Champ créé par un dipôle 1/1
Partie
Question
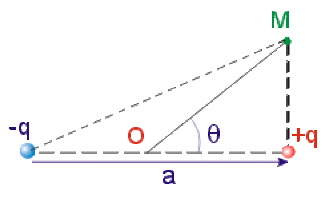
Un dipôle électrostatique est formé de deux charges \(-q\) et \(+q\) . Soit \(a\) la distance entre les charges. On cherche le champ \(\vec E\) existant en \(M\) à une distance \(r \gg a\). On appelle \(\theta\) l'angle \((\vec a, \overrightarrow{OM})\), \(\vec a\) étant orienté de \(-q\) vers \(+q\) . On démontre que le potentiel en \(M\) est la fonction de \(r\) et de \(\theta\) suivante :
\(V = \frac{1}{4 \pi \epsilon_0} \frac{q ~ a}{r^2} ~ \cos \theta\) .
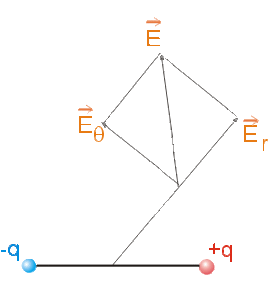
a) Quelles sont les composantes \(E_r\) et \(E_{\theta}\) du champ. Quel est le module du champ?
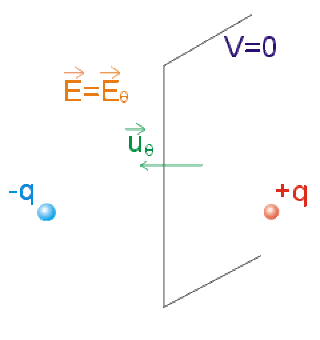
b) Quelle est la forme de l'équipotentielle \(V = 0\) ?
c) Quelle est la direction du champ \(\vec E\) pour \(\theta = \pi /2\) ?
Solution détaillée
a)
\(E_r = - \frac{\partial V}{\partial r} = \frac{1}{4 \pi \epsilon_0} \frac{2 q a ~ \cos \theta}{r^3}\)
\(E_{\theta} = - \frac{1}{r} \frac{\partial V}{\partial \theta} = \frac{1}{4 \pi \epsilon_0} \frac{2 q a ~ \sin \theta}{r^3}\)
\(||\vec E||=\sqrt{E_r^2+E_{\theta}^2}=\frac{qa}{4\pi\epsilon_0r^3}\sqrt{1 + 3 \cos^2 \theta}\)
b)
\(V = 0\) pour \(\cos \theta = 0\) : \(\theta = \frac{\pi}{2}\) . La surface équipotentielle \(V = 0\) est le plan médiateur du dipôle.
c)
\(E_r = 0\) ;
\(E_{\theta} = \frac{qa}{4 \pi \epsilon_0 r^3}\)
Seule existe la composante orthoradiale \(E_{\theta}\)
Le champ \(\vec E\) est bien orthogonal à la surface équipotentielle \(V = 0\) .