Exercice 3
Durée : 5 mn
Note maximale : 10
Question
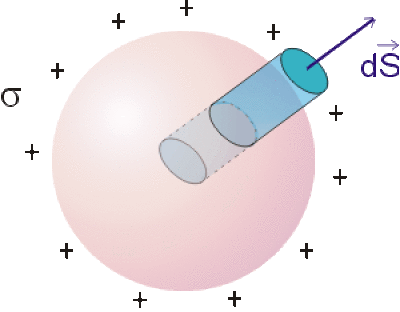
Calculer le flux de \(\vec E\) à travers un cylindre de section infiniment petite \(dS\), enfoncé complètement dans un conducteur ( de façon à ce que \(dS\) soit au voisinage immédiat du conducteur).
En appliquant le théorème de Gauss, déduire le champ \(\vec E\) au voisinage du conducteur en fonction de la densité superficielle de charges \(\sigma\) portée par celui-ci.
Solution
\(\vec E=0\) à l'intérieur du conducteur. Donc le flux à travers la surface du cylindre intérieur est nulle ( en pointillé sur la figure).
\(\vec E\) perpendiculaire au conducteur au voisinage de sa surface. Donc le flux à travers la surface latérale est nul.
Il reste le flux à travers \(dS\) : \(d\Phi=\vec E.d\vec S=E.dS\)
La charge intérieure au cylindre est : \(dq=\sigma dS\)
théorème de Gauss : \(E.dS=\frac{\sigma.dS}{\epsilon_0}\rightarrow E=\frac\sigma{\epsilon_0}\) 10pts