Effet d'un diélectrique
Le coefficient de la capacité d'un condensateur à air de dimensions ordinaires est faible. On l'augmente en interposant un diélectrique entre les armatures. Nous allons étudier comment le diélectrique agit en prenant pour exemple le condensateur plan.
Etablissons une d.d.p. \(V_A - V_B > 0\) entre les armatures \(\mathrm A\) et \(\mathrm B\). Puis, ce condensateur étant chargé, isolons les armatures. Elles conservent leur charge \(Q_A\) et \(Q_B\) et la d.d.p. ne varie pas.
La capacité est : \(C = \frac{Q_A}{V_A - V_B}\)
Glissons maintenant une lame \(L\) de diélectrique entre les armatures (voir la figure). Les charges \(Q_A\) et \(Q_B\) des armatures qui sont isolées ne varient pas. Mais le champ électrique dans l'espace occupé par la lame \(L\) a diminué. La d.d.p. \(V_A - V_B\) entre les armatures étant égale à la circulation du champ électrique a donc diminué et la capacité du condensateur a augmenté. Afin de calculer cette capacité, déterminons le champ électrique dans la lame. Appliquons le théorème de Gauss à la surface fermée, représentée ci-dessous.
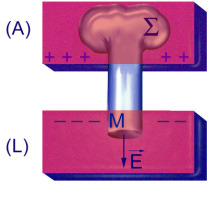
C'est un tube de champ élémentaire limité par une surface (\(\Sigma\)) tracée dans le conducteur (\(\mathrm A\)) et par une section droite au point \(M\) du diélectrique où l'on se propose de déterminer le champ total \(\vec E\).
Désignons par \(\sigma_A\) la densité de charge sur le conducteur \(\mathrm A\) ; d'autre part, elle est négative sur la face de la lame (\(\mathrm L\)) située vis-à-vis du conducteur (\(\mathrm A\)) et vaut \(-P\). On obtient immédiatement en appliquant le théorème de Gauss :
\(F = \frac{\sigma_A ~ - ~ P}{\epsilon_0}\)
Si le diélectrique est parfait :
\(P = \chi ~ \epsilon_0 ~ E\)
et on obtient en éliminant \(P\) de la relation précédente :
\(E = \frac{\sigma_A}{\epsilon_0~(1+\chi)}\)
Supposons que le diélectrique occupe tout l'espace compris entre les armatures. La différence de potentiel entre les armatures vaut :
\(V_A - V_B = E ~ d = \frac{\sigma_A}{\epsilon_0~(1+\chi)} ~ d\)
L'armature (\(\mathrm A\)) d'aire \(S\) porte la charge \(Q_A = S ~ \sigma_A\) . La capacité du condensateur vaut donc :
\(C = \frac{Q_A}{V_A - V_B} = S ~ \sigma_A ~ \frac{\epsilon_0~(1 + \chi)}{\sigma_A~.~d}\)
On en arrive à :
\(C = \epsilon_0~(1 + \chi) ~ \frac S d\)
On pose :
\(\epsilon = \epsilon_0~(1 + \chi)\)
\(\chi\) : susceptibilité électrique du diélectrique.
\(\epsilon\) est appelée constante diélectrique ou permittivité de la substance (pour le vide \(\chi = 0\) et on obtient \(\epsilon = \epsilon_0\)). En définitive, l'expression de la capacité d'un condensateur est :
\(C = \epsilon ~ \frac S d\)
Si l'espace compris entre les armatures est vide \(\epsilon = \epsilon_0\) et la capacité vaut \(C_0 = \epsilon_0 ~ \frac S d\), on obtient, en faisant le quotient membre à membre de ces deux relations :
\(C = \epsilon_r~C_0\), étant posé \(\epsilon_r = \frac{\epsilon}{\epsilon_0} = 1+\chi\)
On appelle \(\epsilon_r\) la constante diélectrique relative. En remplissant entièrement l'espace compris entre les armatures d'un condensateur par un isolant de constante diélectrique relative \(\epsilon_r\), on multiplie la capacité de ce condensateur par \(\epsilon_r\). Ce résultat que nous avons établi dans le cas du condensateur plan est valable pour tous les condensateurs. Voici des valeurs de \(\epsilon_r\) :
air (0°) : 1,00059
eau (20°C) : 80
huile de transformateur : 2,2
mica : 5,5
verre Pyrex : 4,0