Association de condensateurs
En série
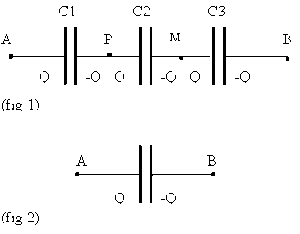
Ce montage est représenté (figure 1) dans le cas de 3 condensateurs.
Ces condensateurs étant initialement déchargés, on applique une d.d.p. \(V_A - V_B\) entre les bornes \(\mathrm A\) et \(\mathrm B\). L'armature du condensateur \(C_1\), reliée à la borne \(\mathrm A\), reçoit une certaine quantité d'électricité \(Q\), positive. Les autres armatures portent les charges \(Q\) ou \(-Q\), qui sont réparties comme il est indiqué (figure 1). En effet, les deux armatures d'un condensateur portent des quantités d'électricité opposées.
D'autre part, le conducteur formé en reliant l'armature d'un condensateur à l'armature du condensateur suivant est électriquement isolé ; la quantité d'électricité de ce conducteur est donc constante ; elle reste nulle au cours du processus de charge ; des quantités d'électricité opposées apparaissent sur ces armatures parce que la répartition des charges électriques dans ce conducteur isolé se modifie au cours du processus de charge. On remarque que les quantités d'électricité fournie sont \(+Q\) sur l'armature reliée au point \(\mathrm A\) et \(-Q\) sur l'armature reliée au point \(\mathrm B\) .
Déterminons la capacité \(C\) du conducteur équivalent au montage des condensateurs en série. Si l'on applique la même d.d.p. \(V_A - V_B\) au condensateur équivalent, les mêmes quantités d'électricité \(Q\) et \(-Q\) sont reçues par ses armatures (figure 2). Sa capacité \(C\) est donc telle que :
(1) \(~Q=C (V_A - V_B)\)
Considérant le montage en série (figure 1) des condensateurs de capacités \(C_1\), \(C_2\) et \(C_3\) , on peut écrire pour chacun d'eux :
\(~Q=C_1 (V_A - V_P)\)
\(~Q=C_2 (V_P - V_M)\)
\(~Q=C_3 (V_M - V_B)\)
et par suite :
\(\frac{Q}{C_1} + \frac{Q}{C_2} + \frac{Q}{C_3} = (V_A - V_P) ~+~ (V_P - V_M) ~+~ (V_M - V_B) = V_A - V_B = \frac Q C~~~~(2)\)
On obtient immédiatement :
\(\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}\)
D'une manière générale, si \(n\) condensateurs de capacités \(C_1, C_2, ...., C_n\) , sont montés en série, le condensateur équivalent a la capacité \(C\) telle que :
\(\displaystyle{\frac{1}{C} = \sum_{i=1}^n \frac{1}{C_i}}\)
En parallèle
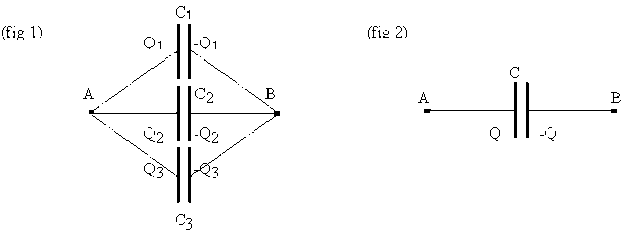
On a représenté (figure 1) le montage en parallèle de 3 condensateurs de capacité \(C_1\), \(C_2\) et \(C_3\). La même d.d.p. est appliquée à tous les condensateurs. Les armatures reliées au point \(\mathrm A\) prennent les quantités d'électricité \(Q_1\), \(Q_2\) et \(Q_3\), positives si \(V_A > V_B\). Les armatures reliées au point \(\mathrm B\) prennent les quantités d'électricité \(-Q_1\), \(-Q_2\) et \(-Q_3\).
Si la même d.d.p. \(V_A - V_B\) est appliquée au condensateur équivalent (figure 2), à ce montage, son armature chargée positivement reçoit la quantité d'électricité \(Q_1 + Q_2 + Q_3\). La capacité \(C\) de ce condensateur est donc telle que :
\((1) ~~~~ Q_1+Q_2+Q_3=C(V_A-V_B)\)
On peut écrire pour chaque condensateur du montage en parallèle :
\(~Q_1=C_1 (V_A - V_B)\)
\(~Q_2=C_2 (V_A - V_B)\)
\(~Q_3=C_3 (V_A - V_B)\)
La relation (1) s'écrit donc : \(C_1(V_A-V_B)+C_2(V_A-V_B)+C_3(V_A-V_B)\)
Il vient après simplification : \(C = C_1+C_2+C_3\)
D'une manière générale, la capacité \(C\) du condensateur équivalent à \(n\) condensateurs montés en parallèle, de capacité \(C_1, C_2, ...., C_n\) est :
\(\displaystyle{C = \sum_{i=1}^n C_i}\)