Lignes de champ et surfaces équipotentielles du dipôle
Les lignes de champ créées par le dipôle
Les lignes de champ électrique au voisinage du dipôle partent de la charge \(+q\) et arrivent à la charge \(- q\) comme représentées sur la figure ci-dessous.
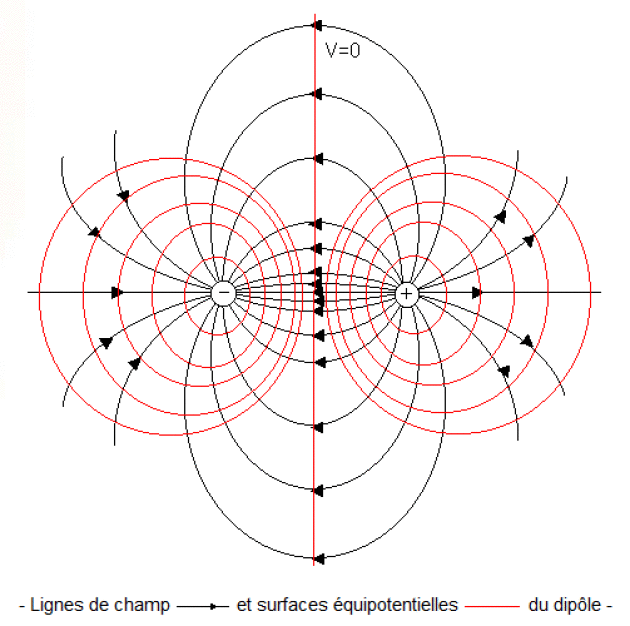
Les surfaces équipotentielles d'un dipôle
Les surfaces équipotentielles \(V = \mathrm {constante}\) sont caractérisées par la relation \(\mathrm d V = 0\). Si l'on rapproche ce résultat de la relation champ potentiel :
\(\mathrm d V = 0 = - \vec E. \mathrm d \vec l\) ,
il apparaît un résultat important à savoir que les surfaces équipotentielles sont orthogonales aux lignes de champ. On se reportera dans le cas du dipôle à la figure ci-dessus où sont représentées les lignes de champ orthogonales aux équipotentielles.
Au voisinage d'une charge, son potentiel (qui varie comme \(1/r\) ) l'emporte sur le potentiel de l'autre charge. La surface équipotentielle est pratiquement une sphère.
Le plan médiateur du dipôle qui est le lieu géométrique des points équidistants des deux charges est une équipotentielle \(V = 0\).
Loin des charges, pour \(r \gg a\) dans les conditions du calcul du potentiel du dipôle, les surfaces équipotentielles \(V = \mathrm {constante}\) ont pour équation : \(r^2 = \mathrm {Constante} ~ . ~ \cos \theta\)