Effet dipolaire

Les Molécules de dipôle permanent :

La structure de la molécule est telle qu'en permanence le barycentre des charges \(+\) (les noyaux) est distinct de celui des charges \(-\) (les électrons). La molécule est "polaire".

• Les Molécules diatomiques :

Dans la molécule \(\mathrm H - \mathrm{Cl}\) le nuage d'électrons est déformé vers \(\mathrm {Cl}\) et il en résulte un moment dipolaire permanent :

\(p ( \mathrm H - \mathrm{Cl} )= 1.03 ~ \mathrm D\)

De même dans la molécule d'oxyde de carbone \(\mathrm C - \mathrm O\), l'atome d'oxygène est ''accepteur'' d'électrons tandis que l'atome de carbone est ''donneur'' d'électrons. Le centre des charges négatives est déplacé vers l'atome d'oxygène et il existe un moment dipolaire permanent :

\(p (\mathrm C - \mathrm O) = 0.12 ~ \mathrm D\)

• Les Molécules polyatomiques :

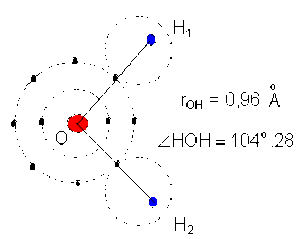
Exemple de la molécule d'eau :

Autres exemples de molécules polyatomiques :

\(\mathrm H \mathrm C \mathrm N\) linéaire \(p = 2.95 ~ \mathrm D\)

\(\mathrm {NH}_3\) pyramidale \(p = 1.47 D\)

\(\mathrm H_2 \mathrm O\) angulaire \(p = 1.84 ~ \mathrm D\)

Dans le cas des molécules polyatomiques, si nous connaissons la structure d'une molécule ainsi que le moment \(\vec p_i\) de chaque liaison, il est possible de déterminer le moment dipolaire résultant \(\vec p\) de la molécule :

\(\displaystyle{\vec p = \sum_i \vec p_i}\)

Les Molécules non polaires :

La répartition des charges dans ces molécules est telle que les barycentres des charges \(+\) et \(-\) sont confondus. C'est le cas :

• des molécules à liaisons purement covalentes où il y a un égal partage des électrons : \(\mathrm H_2\), \(\mathrm N_2\), \(\mathrm {Cl}_2\)

• des molécules dont les moments dipolaires partiels se compensent en raison de la symétrie de la molécule :

  \(\mathrm {CO}_2\) linéaire \(~ \mathrm {BF}_3\) triangulaire \(~\mathrm C_6 \mathrm H_6\) hexagonale

En présence d'un champ électrique extérieur il s'exerce des forces de sens contraire sur les charges \(+\) et \(-\) d'un atome ou d'une molécule. Il apparaît une séparation des barycentres des charges \(> 0\) et \(< 0\).

L'atome ou la molécule sont alors dits polarisables et nous avons un moment dipolaire "induit" par la présence du champ électrique. A noter qu'un tel champ électrique peut être créé par un dispositif formé de deux plaques portant des charges opposées mais aussi par une molécule polaire voisine de la molécule influencée.

La polarisation, proportionnelle au champ électrique se traduit par un moment dipolaire induit \(\vec p\).

• Dans le cas des atomes :

\(\vec p = \alpha \vec E\)

\(\alpha\) est le coefficient de polarisabilité. Il dépend du numéro atomique \(Z\) de l'atome. Il s'exprime en \(\mathrm {C.m}^2. \mathrm V^{-1}\).

• Dans le cas des molécules :

\(\vec p = \alpha_m \vec E\)

\(\alpha_m\) est le coefficient de polarisabilité de la molécule.

En fait dans tout atome ou molécule les électrons sont animés d'un mouvement permanent et à un instant donné les barycentres des charges \(+\) et \(-\) ne coïncident pas. Il existe à chaque instant des dipôles instantanés : \(\vec p (t)\) .

Bien que nous ayons en moyenne au cours du temps :

\(\langle \vec p (t) \rangle = \vec 0\) ,

il n'en demeure pas moins que les atomes ou les molécules sont en interaction permanente.

La mesure du moment dipolaire d'une molécule conduit a des informations importantes concernant :

• la forme des molécules (Ex : \(\mathrm C_6 \mathrm H_6\) dont le moment dipolaire est nul et la structure en moyenne hexagonale).

• La nature des liaisons atomiques (Ex : détermination des isomères qui présentent la même formule générale mais dont les liaisons sont de nature différente).

• Origine et nature des forces de cohésion :

Dans la matière, les dipôles permanents et instantanés créent un champ qui interagit avec les molécules déformables et fait apparaître des dipôles induits. Le bilan des interactions entre les dipôles a pour conséquence une force attractive appelée interaction de Van der Waals. Cette action est responsable de la grande cohésion des molécules entre elles au sein de la matière.

La force d'attraction dépend très fortement de la distance \(r\) entre les molécules. L'énergie potentielle variant en \(1/r^6\) , la force de Van der Waals qui dérive de cette énergie potentielle varie comme \(1/r^7\) .

• Conséquences des forces de cohésion en chimie

Une solution étant formée d'un solvant et d'un soluté la solvatation résulte de l'association des molécules de solvant avec une molécule ou un ion de soluté. Lors de la dissolution les composés ioniques ne se dissolvent que dans des solvants très polaires comme l'eau, les alcools ... .

On notera par exemple la dissolution de \(\mathrm{Na} - \mathrm{Cl}\) dans l'eau. Les ions \(\mathrm{Na}^+\) et \(\mathrm {Cl}^-\) sont solvatés par l'eau.

L'hydratation est un cas particulier de solvatation pour lequel les molécules de solvant sont les molécules d'eau.

• Forces de cohésion en biologie

Au cours du phénomène de solvatation les ions \(\mathrm{Ca}^{++}\) , \(\mathrm{Mg}^{++}\) , \(\mathrm{Na}^+\) , \(\mathrm K^+ \mathrm{Cl}^-\) , présents dans les tissus se déplacent dans l'eau. Au cours de leur mouvement ceux-ci sont freinés par les couches de solvatation.

• Par un champ électrique : origine de la constante diélectrique

Un matériau placé dans un champ \(\vec E\) peut être polarisé. Ses molécules ou ses atomes deviennent des dipôles orientés dans le sens de \(\vec E\).

• Effet d'une contrainte : Piezoélectricité.

Le phénomène de polarisation apparaît dans certains cristaux, comme le quartz, sous l'effet d'une contrainte mécanique.

Au repos, le moment dipolaire du cristal est nul \(\vec p = 0\). Sous l'effet d'une contrainte la direction des moments de certaines liaisons se trouve modifiée et nous avons \(\vec p ¹ 0\) .

L'arrangement étant régulier, des charges de signes opposés apparaissent de part et d'autre créant un champ parallèle à la contrainte.

Sur le plan expérimental mentionnons que la valeur du signal électrique mesuré permet d'évaluer la valeur de la contrainte.

• Polarisation d'une fibre nerveuse (ou musculaire) :

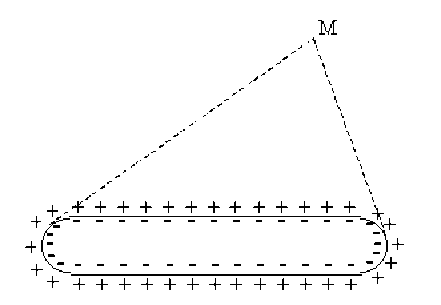
Au repos la membrane d'une fibre nerveuse est polarisée. Celle-ci peut être représentée par un grand nombre de dipôles dont les moments sont opposés 2 à 2. Le champ et le potentiel en un point \(M\), à une certaine distance, sont nuls.

L'influx nerveux se traduit par la dépolarisation de la fibre par changement de la concentration des ions de part et d'autre de la membrane.

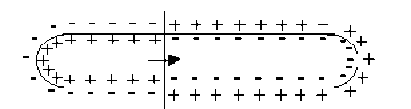
La propagation de l'influx nerveux se traduit par une onde de dépolarisation le long de la fibre nerveuse.

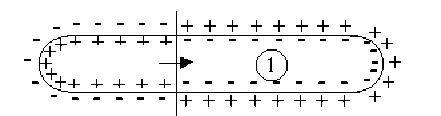
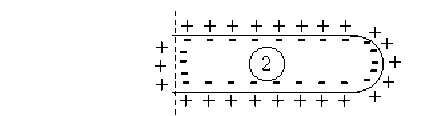
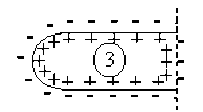
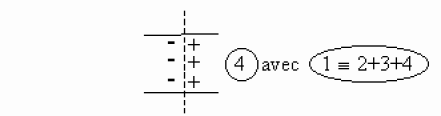
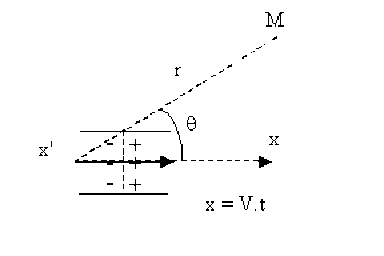
La perturbation représentée par l'onde de dépolarisation se propage le long de la fibre nerveuse à une vitesse \(V\) qui est la vitesse de déplacement de l'influx nerveux.

On remarquera que l'état \(1\) qui figure un état de dépolarisation qui se propage à un instant donné, est équivalent à la somme des états \(2 + 3 + 4\) de la membrane.

Si l'on admet comme précédemment que les états \(2\) et \(3\) ne créent en \(M\) aucun potentiel et aucun champ électrique, il apparaît alors que la propagation de l'influx nerveux peut être associée au déplacement d'un dipôle électrique selon l'axe de la fibre nerveuse à la célérité \(V\).

Le potentiel électrique en un point \(M\) est donné par la relation :

\(V(M) = k \frac{p.\cos\theta}{r^2}\)

ou encore \(V(M) = k \frac{\vec p . \vec r}{r^3}\)

• Principe de l'Electrocardiogramme. E.C.G.

Nous avons là un exemple fondamental de la notion de dipôle liée à la propagation de l'influx nerveux.

L'activité périodique du coeur commence par une dépolarisation des cavités supérieures ou oreillettes ; elle est suivie de la dépolarisation des cavités inférieures ou ventricules. L'électrocardiogramme est basé sur le principe de la polarisation et de la dépolarisation du muscle cardiaque.

L'électrocardiogramme est obtenu en mesurant en différents points du corps humain les potentiels créés par les ondes de dépolarisation et de repolarisation.

Le vectocardiogramme.

L'activité du muscle cardiaque peut sur le plan des phénomènes électriques être perçue comme le changement d'orientation d'un vecteur dipôle électrique au cours des différentes phases du cycle.

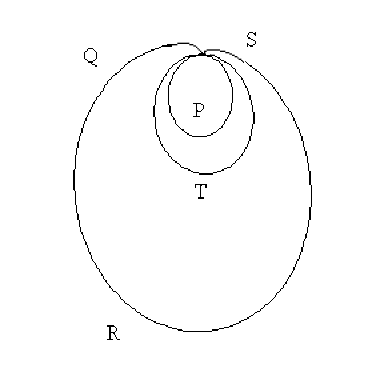
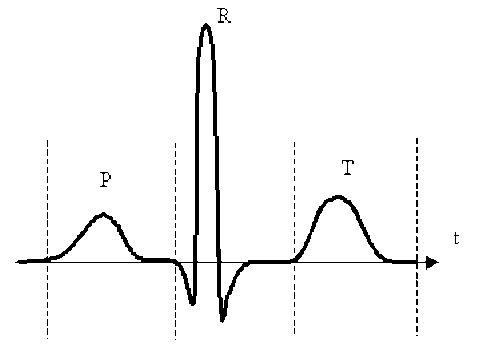
La figure ci-dessus reproduit l'orientation et l'intensité du vecteur dipôle électrique, aussi appelé vectocardiogramme, au cours d'un cycle du muscle cardiaque.

La petite boucle \(P\) est à associer à l'activité des oreillettes. La grande boucle \(R\) correspond à l'activation du muscle ventriculaire. Le cycle se termine par une onde de repolarisation du muscle ventriculaire que l'on perçoit sur la boucle \(T\).

Expérimentalement les potentiels mesurés sont de quelques millivolts.

La figure ci-dessous représente schématiquement le tracé d'un électrocardiogramme qui correspond aux mesures de tensions enregistrées lors des cycles \(P\),\(R\) et \(T\).