Loi des actions électrodynamiques d'Ampère
Elle est à la magnétostatique ce que la loi de Coulomb[1] (biographie de : Coulomb[2]) est à l'électrostatique.
Soient, dans le vide, deux circuits rigides filiformes \(\mathfrak D_1\) et \(\mathfrak D_2\) immobiles par rapport à un référentiel \(\mathcal{R}\) et parcourus respectivement par des courants continus d'intensités \(I_1\) et \(I_2\).
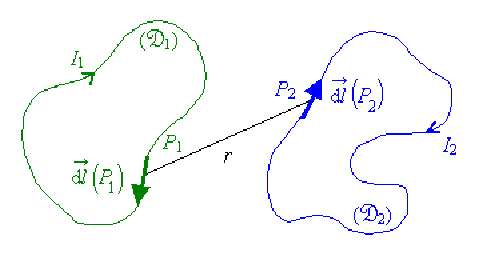
L'interaction électromagnétique entre ces deux circuits se manifeste par une force \(\vec F_{1 \leftarrow2}\) exercée par
\(\displaystyle{\vec F_{1 \leftarrow2} = \frac {\mu_0}{4\pi}I_1I_2\int_{\mathfrak{D}_1}\int_{\mathfrak{D}_2}\overrightarrow{\mathrm{d}l}(P_1) \wedge\Big [\overrightarrow {\mathrm{d}l} (P_2) \wedge \frac{\overrightarrow {P_2P_1}}{r^3}\Big]}\)
ou
\(\displaystyle{\vec F_{1 \leftarrow2} = \frac {\mu_0}{4\pi}\int_{\mathfrak{D}_1}\int_{\mathfrak{D}_2}I_1\overrightarrow{\mathrm{d}l}(P_1) \wedge \Big[I_2\overrightarrow {\mathrm{d}l} (P_2) \wedge \frac{\overrightarrow {P_2P_1}}{r^3}\Big]}\)
Comme sous le second signe somme \(\int_{\mathfrak D_2}\), \(P_1\) est un point fixe et \(P_2\) un point courant[3], on peut écrire l'expression précédente sous la forme :
\(\displaystyle{\vec F_{1 \leftarrow2} = \int_{\mathfrak{D}_1}I_1\overrightarrow {\mathrm{d}l}(P_1) \wedge \int_{\mathfrak{D}_2}\frac {\mu_0}{4\pi}I_2\overrightarrow {\mathrm{d}l}(P_2) \wedge \frac {\overrightarrow {P_2P_1}}{r^3}}\) avec \(\vec r = \overrightarrow {P_2P_1}\)
De même pour la force qui s'exerce sur \(\mathfrak{D}_2\), on a :
\(\displaystyle{\vec F_{2 \leftarrow1} = \frac {\mu_0}{4\pi}I_1I_2\int_{\mathfrak{D}_1}\int_{\mathfrak{D}_2}\overrightarrow{\mathrm{d}l}(P_2) \wedge\Big [\overrightarrow {\mathrm{d}l} (P_1) \wedge \frac{\overrightarrow {P_1P_2}}{r^3}\Big]}\)
ou
\(\displaystyle{\vec F_{2 \leftarrow1} =\int_{\mathfrak{D}_2} I_2 \overrightarrow{\mathrm{d}l}(P_2)\wedge\int_{\mathfrak{D}_1} \frac {\mu_0}{4\pi}I_1\overrightarrow{\mathrm{d}l}(P_1)\wedge \frac{\overrightarrow {P_1P_2}}{r^3}}\) avec \(\vec r = \overrightarrow {P_1P_2}\)
\(\mu_0\) est un coefficient caractéristique du vide appelé perméabilité du vide, \(\mu_0 = 4\pi 10^{-7}\mathrm{H} . \mathrm{m}^{-1}\)