Calcul de dA, cas d'un fil rectiligne
Partie
Question
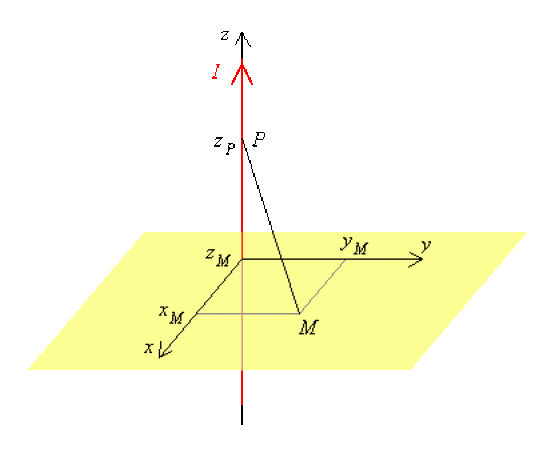
On considère un conducteur rectiligne et filiforme parcouru par un courant d'intensité constante égale à \(I\).
Considérons le repère \(\mathcal{R} = (0 ; x, y, z)\) tel que le conducteur est porté par l'axe \(Oz\). Soient \(M\) un point quelconque de coordonnées \(\left(x_M, y_M, z_M\right)_{\mathcal{R}}\), et \(P\) un point du conducteur de coordonnées \(\left(0, 0, z_P\right)_{\mathcal{R}}\).
Déterminer quel est le potentiel vecteur élémentaire \(\vec{\mathrm{d}A}\) créé en \(M\) par une longueur de conducteur élémentaire \(\vec{\mathrm{d}l}\) orientée dans le sens de \(I\) et centrée en \(P\).
Rappel de cours
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
On sait que \(\displaystyle{ \vec{\mathrm{d}A} = \frac{\mu_0}{4 \pi} \frac{I . \vec{\mathrm{d}l} }{PM} }\), il faut alors calculer \(PM\).
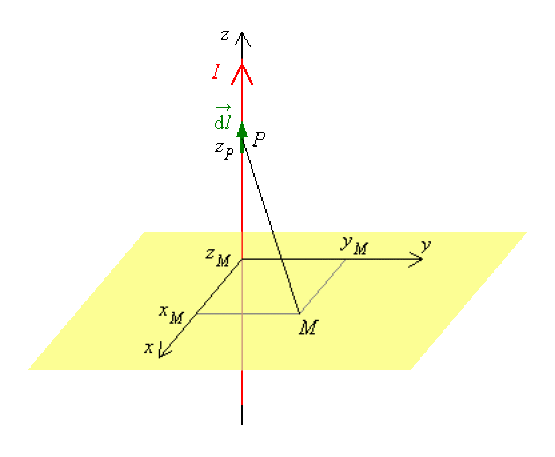
On a
\(\vec{PM} \mathrm{ } \left| \begin{array}{l} x_M - 0 \\ y_M - 0 \\ z_M - z_P \end{array}\right.\) \(\Rightarrow PM = \sqrt{x_M^2 + y_M^2 + (z_M - z_P)^2}\)
D'où \(\displaystyle{ \vec{\mathrm{d}A} = \frac{\mu_0}{4 \pi} \cdot \frac{I . \vec{\mathrm{d}l} }{ \sqrt{x_M^2 + y_M^2 + (z_M - z_P)^2} } }\)