Les propriétés du champ magnétostatique

On appelle divergence au point \(\mathsf{M}\) du champ vectoriel \(\vec B(M)\), le scalaire que l'on note \(\mathrm{div}\vec B(M)\) défini par la formule d'Ostrogradski :

\(\oiint_{\mathfrak{S}} \vec B(M_{\mathfrak{S}}) . \overrightarrow{\mathrm{d}\mathfrak{S}} (M_{\mathfrak{S}}) = \iiint_{\mathfrak{V}} \mathrm{div} \vec B(M_{\mathfrak{V}}) \mathrm{d}\mathfrak{V}(M_{\mathfrak{V}})\)

\(M_{\mathfrak{S}}\) étant un point de la surface fermée \(\circledS\) et \(M_{\mathfrak{V}}\) un point du volume \((\mathfrak{V})\) délimité par \(\circledS\).

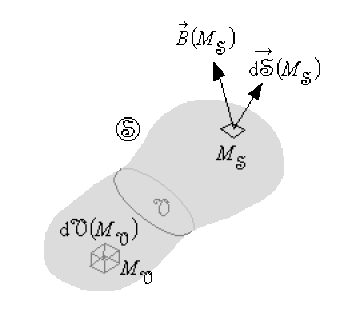
Le flux du champ vectoriel \(\vec B(M)\) à travers une surface fermée quelconque \(\circledS\) est égal à l'intégrale triple du champ scalaire \(\mathrm{div}\vec B(M)\) étendue au volume \((\mathfrak{V})\) délimité par \(\circledS\) .

• L'opérateur divergence fait correspondre à un champ vectoriel \(\vec B(M)\) un champ de scalaire \(\mathrm{div}\vec B(M)\) ; il peut donner des informations sur le caractère "divergent ou convergent" du champ vectoriel \(\vec B(M)\).

L'expression du flux du champ magnétostatique à travers une surface fermée s'écrit :

\(\oiint_{\mathfrak{S}} \stackrel{\hookrightarrow}{B}(M) . \mathrm{ } \overrightarrow{\mathrm{d}\mathfrak{S}}(M) = 0\)

soit, en précisant les notations, \(\oiint_{\mathfrak{S}} \stackrel{\hookrightarrow}{B}(M_{\mathfrak{S}}) . \mathrm{ } \overrightarrow{\mathrm{d}\mathfrak{S}}(M_{\mathfrak{S}}) = 0\), \(M_{\mathfrak{S}}\) étant un point de la surface fermée \(\circledS\).

La formule d'Ostrogradski

\(\oiint_{\mathfrak{S}} \stackrel{\hookrightarrow}{B}(M_{\mathfrak{S}}). \mathrm{ } \overrightarrow{\mathrm{d}\mathfrak{S}}(M_{\mathfrak{S}}) = \iiint_{\mathfrak{V}}\mathrm{div} \stackrel{\hookrightarrow}{B}(M_{\mathfrak{V}})\mathrm{d} \mathfrak{V}(M_{\mathfrak{V}}) = 0\),

\(M_{\mathfrak{V}}\) étant un point du volume déterminé par \(\circledS\), permet d'obtenir la relation qui établit la conservativité du flux du champ magnétostatique, soit :

\(\iiint_{\mathfrak{V}}\mathrm{div} \stackrel{\hookrightarrow}{B}(M)\mathrm{d}\mathfrak{V} = \oiint_{\mathfrak{S}} \stackrel{\hookrightarrow}{B}(M) . \mathrm{ } \overrightarrow{\mathrm{d}\mathfrak{S}} = 0\)

et qui permet d'écrire l'équation locale \(\mathrm{div} \vec B(M) = 0\)