Moment magnétique d'un circuit - Expression du potentiel vecteur [Les courants stationnaires : champ et potentiel vecteur magnétostatiques]

Moment magnétique d'un circuit - Expression du potentiel vecteur

Définition du moment magnétique d'un circuit filiforme

Définition :

On appelle moment magnétique d'un circuit la grandeur définie par l'expression :
\(\mathcal{M} = I \iint_{\mathfrak{S}}\mathrm{d}\mathfrak{S}\)
Il est exprimé en ampère mètre carré \((\mathrm{A} . m^2)\).

Expression du moment magnétique d'un circuit

La relation précédente est valable quelle que soit la surface \(\mathfrak{S}\) s'appuyant sur le contour du circuit \(\mathsf{C}\), le vecteur surface^[1] \(\stackrel{\hookrightarrow}{\mathfrak{S}} = \iint_{\mathfrak{S}} \stackrel{\hookrightarrow}{\mathrm{d}\mathfrak{S}}\) est indépendant de la forme de la surface ouverte qui s'appuie sur \(\mathsf{C}\) : il est caractéristique de ce dernier ; ainsi \(\stackrel{\hookrightarrow}{\mathcal{M}} = I \stackrel{\hookrightarrow}{S}\)

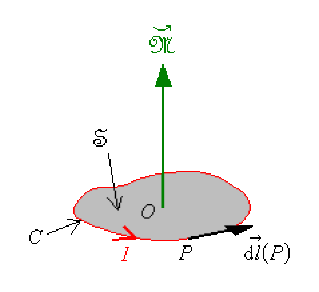
Expression du potentiel vecteur

\(\vec A(M) = \frac{\mu_0}{4\pi} \stackrel{\hookrightarrow}{\mathcal{M}} \wedge \frac{\overrightarrow{OM}}{OM^3}\)

Notes

Vecteur surface
- Soit le champs de vecteurs \(f \vec V\) où \(f\) est un champ de scalaire quelconque et \(\vec V\) un champ vectoriel uniforme quelconque.
  La formule d'Ostrogradski appliquée au champ \(f \vec V\) s'écrit :
  \(\oiint_{\mathfrak{S}}(f \vec V).\vec{\mathrm{d}\mathfrak{S}}=\iiint_{\mathfrak{V}} \mathrm{div} (f \vec V)\mathrm{d}\mathfrak{V}\)
  Puisque \(\vec V\) est un champ uniforme le premier membre donne : \(\oiint_{\mathfrak{S}}(f \vec V).\vec{\mathrm{d}\mathfrak{S}}=\vec V.\oiint_{\mathfrak{S}}f.\vec{\mathrm{d}\mathfrak{S}}\)
  Pour le second membre, la divergence s'écrit :
  \(\mathrm{div} (f \vec V) = f~\mathrm{div}~\vec V~+~\vec V.~\overrightarrow{\mathrm{grad}}~f= \vec V.~\overrightarrow{\mathrm{grad}}~f\) car \(\mathrm{div}~\vec V=0\)
  \(\iiint_{\mathfrak{V}} \mathrm{div} (f \vec V)\mathrm{d}\mathfrak{V}=\iiint_{\mathfrak{V}} \vec V.~\overrightarrow{\mathrm{grad}}~f~\mathrm{d}\mathfrak{V}=\vec V.\iiint_{\mathfrak{V}} ~\overrightarrow{\mathrm{grad}}~f~\mathrm{d}\mathfrak{V}\)
- Ainsi : \(\vec V.\oiint_{\mathfrak{S}}f.\vec{\mathrm{d}\mathfrak{S}}=\vec V.\iiint_{\mathfrak{V}} ~\overrightarrow{\mathrm{grad}}~f~\mathrm{d}\mathfrak{V}\)
  \(\vec V\) étant un champ uniforme quelconque, on obtient la relation :
  \(\oiint_{\mathfrak{S}}f.\vec{\mathrm{d}\mathfrak{S}}=\iiint_{\mathfrak{V}} ~\overrightarrow{\mathrm{grad}}~f~\mathrm{d}\mathfrak{V}\) appelée formule du gradient.
  Si f = 1, la formule du gradient donne : \(\oiint_{\mathfrak{S}}\vec{\mathrm{d}\mathfrak{S}}=\vec 0\).
- Considérons deux surfaces quelconques \(\mathfrak{S}_1\) et \(\mathfrak{S}_2\) s'appuyant sur un contour fermé \(\textcircled{C}\).
  Le sens de parcours arbitrairement choisi sur \(\textcircled{C}\) détermine l'orientation de \(\mathfrak{S}_1\) et \(\mathfrak{S}_2\).
L'ensemble (\(\mathfrak{S}_1~+~\mathfrak{S}_2\)) constitue une surface fermée ; ainsi, l'orientation de \(\mathfrak{S}_2\) est changée, la normale à la surface fermée (\(\mathfrak{S}_1~+~\mathfrak{S}_2\)) étant orientée vers l'extérieur.
La formule du gradient donne donc :
\(\vec{\mathfrak{S}_1}-\vec{\mathfrak{S}_2}=\oiint_{\mathfrak{S}}\vec{\mathrm{d}\mathfrak{S}}=\vec 0\)
Ainsi, le pseudo-vecteur associé à une surface (ouverte) s'appuyant sur un contour fermé \(\textcircled{C}\) est indépendant de la surface choisie et s'écrit donc : \(\stackrel{\hookrightarrow}{\mathfrak{S}}=\iint_{\mathfrak{S}}\stackrel{\hookrightarrow}{\mathrm{d}\mathfrak{S}}\)