Les courants stationnaires : champ et potentiel vecteur magnétostatiques

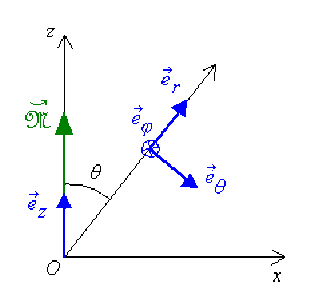
En explicitant le produit vectoriel dans l'expression du potentiel vecteur créé par le dipôle magnétostatique, on a, avec \(\vec r = \overrightarrow{OM}\)  :

\(\vec A(M) = \frac{\mu_0}{4\pi} \stackrel{\hookrightarrow}{\mathcal{M}} \wedge \frac{\overrightarrow{OM}}{OM^3} = \frac{\mu_0}{4\pi}\frac{\mathcal{M}\sin\theta}{r^2}\vec e_{\phi}\) c'est-à-dire : \(\vec A(M) = A_{\phi} \vec e_{\phi}\)

Le rotationnel^[1] du potentiel vecteur s'écrit donc :

\(\displaystyle{ \stackrel{\hookrightarrow}{\mathrm{rot}}\vec A(M) = \Big[\frac{1}{r \sin \theta} \frac{∂}{∂\theta}(A_{\phi}\sin\theta)\Big]\vec e_r - \Big[\frac{1}{r} \frac{∂}{∂r}(rA_{\phi})\Big]\vec e_{\theta}}\)

Ce qui donne pour le champ : \(\displaystyle{ \stackrel{\hookrightarrow}{B}(M) = \frac{\mu_0\mathcal{M}}{4 \pi r^3}\Big[( 2 \cos \theta) \vec e_r + (\sin \theta) \vec e_{\theta}\Big]}\)