Calcul de B sur l'axe d'un solénoïde
Partie
Question
On considère un solénoïde d'axe \(Oz\), de centre \(O\), de rayon \(a\) et de longueur \(2L\). Il comporte \(n\) spires par unité de longueur qui sont parcourues par un courant d'intensité \(I\) constante. L'orientation du courant est donnée par la figure :
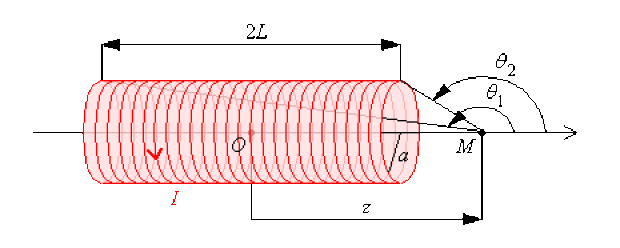
Afin de calculer le champ magnétostatique, le solénoïde sera décomposé en portions élémentaires de longueur \(\mathrm{d}s\) dont on peut donner la contribution \(\vec{\mathrm{d} B}(M)\) en généralisant les résultats de la spire : \(\displaystyle{ \vec{\mathrm{d} B}(M) = n . \mathrm{d}s \frac{\mu_0 I}{2 a} \sin^3 \theta(s) . \vec{e_z} }\) puisqu'il y a \(n . \mathrm{d}s\) spires dans cet élément.

Exprimer le champ magnétostatique en un point \(M\) de l'axe \(Oz\) repéré par \(z = \overline{OM}\) en fonction des deux angles \(\theta_1\) et \(\theta_2\) sous lesquels le solénoïde est vu.
Aide simple
Il faut sommer les contributions élémentaires. Comme \(\theta\) varie avec \(s\), il faut expliciter le lien entre ces deux variables pour en éliminer une dans l'intégrale.
Rappel de cours
Le produit scalaire :
\(\vec A.\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} . \left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =A_1B_1+A_2B_2+A_3B_3\)
Le produit vectoriel :
\(\vec A\wedge\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} \wedge\left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =\left(\begin{array}{c} A_2B_3-A_3B_2\\A_3B_1-A_1B_3\\A_1B_2-A_2B_1\end{array} \right)_{\mathcal{B}}\)
Les opérateurs vectoriels :
Système de repérage cartésien \(\mathcal{B}_{\mathrm{cart.}}(\vec{e_x}, \vec{e_y}, \vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial x} } \\ \displaystyle{ \frac{\partial U}{\partial y} } \\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) | \(\displaystyle{ \frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z} } \\ \displaystyle{ \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x} } \\ \displaystyle{ \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y} }\end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) |
Système de repérage cylindrique \(\mathcal B_{\mathrm{cyl.}}(\vec{e_r},\vec{e_{\theta}},\vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial r} } \\ \displaystyle{ \frac{1}{r} \frac{\partial U}{\partial \theta} }\\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) | \(\displaystyle{ \frac{1}{r} \frac{\partial (r . A_r) }{\partial r} + \frac{1}{r} \frac{\partial A_{\theta}}{\partial \theta}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{1}{r} \frac{\partial A_z}{\partial \theta}-\frac{\partial A_ \theta}{\partial z} } \\ \displaystyle{ \frac{\partial A_r}{\partial z}-\frac{\partial A_z}{\partial r} } \\ \displaystyle{ \frac{1}{r} \left( \frac{\partial (r. A_{\theta})}{\partial r}-\frac{\partial A_r}{\partial \theta} \right)} \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) |
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
La détermination du champ magnétostatique sur l'axe du solénoïde passe par la sommation de toutes les contributions élémentaires et il vient :
\(\displaystyle{ \vec B(M) = \int_{\mathcal{D}} \vec{\mathrm{d} B}(M) = \int_{-L}^L n . \mathrm{d}s \frac{\mu_0 I}{2 a} \sin^3 \theta (s) . \vec{e_z} = \frac{\mu_0 . n . I}{2 a} \int_{-L}^L \sin^3 \theta (s) . \mathrm{d}s . \vec{e_z} }\)
Pour effectuer ce calcul, il faut expliciter \(\mathrm{d}s\) en fonction de \(\theta\) et \(\mathrm{d} \theta\).

\(\begin{array}{lll} \displaystyle{\tan(\pi - \theta) = - \tan \theta = \frac{a}{z - s} } & \Rightarrow & z - s = - a . \cot \theta \\ & \Rightarrow & \displaystyle{- \mathrm{d}s = \frac{a . \mathrm{d} \theta}{\sin^2 \theta} } \\ & \Rightarrow & \displaystyle{ \mathrm{d}s = - \frac{a . \mathrm{d} \theta}{\sin^2 \theta} } \end{array}\)
puisque \(\mathrm{d}z = 0\) (car \(M\) est fixe) et \(\displaystyle{ \frac{\mathrm{d} (\cot \theta)}{\mathrm{d} \theta} = \frac{\mathrm{d} \left( \frac{\cos \theta}{\sin \theta} \right)}{\mathrm{d} \theta} = - \frac{1}{\sin^2 \theta} }\)
On constate une simplification des sinus dans le calcul dans la mesure où les angles limites (\(\theta_1\) correspondant à \(s = - L\) et \(\theta_2\) correspondant à \(s = L\)) sont connus :
\(\begin{array}{lll} \vec B(M) & = & \displaystyle{ \frac{\mu_0 . n . I}{2 a} \int_{\theta_1}^{\theta_2} \sin^3 \theta (s) . \left( - \frac{a . \mathrm{d} \theta}{\sin^2 \theta} \right) . \vec{e_z} } \\ & = & \displaystyle{ - \frac{\mu_0 . n . I}{2} \int_{\theta_1}^{\theta_2} \sin \theta . \mathrm{d} \theta . \vec{e_z} } \\ & = & \displaystyle{ \frac{\mu_0 . n . I}{2} ( \cos \theta_2 - \cos \theta_1 ) . \vec{e_z} } \end{array}\)
L'expression du champ magnétostatique sur l'axe d'un solénoïde fini et vu sous les angles \(\theta_1\) et \(\theta_2\) est :
\(\displaystyle{ \vec B(M) = \frac{\mu_0 . n . I}{2} ( \cos \theta_2 - \cos \theta_1 ) . \vec{e_z} }\)
Remarque :
La première expression de \(\vec B(M)\) sous forme intégrale dépend de \(\theta\) (par \(\sin^3 \theta\)) et de \(s\) (par \(\mathrm{d}s\)). L'intégration nécessite d'expliciter l'une de ces grandeurs en fonction de l'autre pour l'éliminer.
Nous avons choisi d'éliminer \(s\) ; un autre choix consiste à expliciter \(\sin^3 \theta\) en fonction de \(s\) pour éliminer \(\theta\) :
\(\sin\theta=\sin(\pi-\theta)=\frac{a}{PM}=\frac{a}{\sqrt{a^2 + (z - s)^2}}\)
Cela conduit à trouver une primitive de \(\displaystyle{ \frac{a^2}{\left[ a^2 + (z-s)^2 \right]^{3/2} } }\) : ce n'est pas immédiat !