Balance de Cotton
Partie
Question
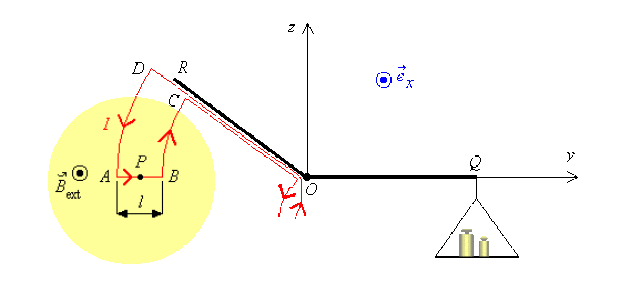
La balance de Cotton est un appareil de mesure du champ magnétostatique. L'un des fléaux est constitué d'un circuit parcouru par un courant d'intensité \(I\) et plongé dans le champ magnétostatique \(\vec B_{\mathrm{ext}}\) à mesurer. Le deuxième fléau permet d'équilibrer la balance à l'aide de masses marquées.
On suppose que :
le champ magnétostatique \(\vec B_{\mathrm{ext}}\) est uniforme et donné par \(\vec B_{\mathrm{ext}} = B_{\mathrm{ext}} . \vec{e_x}\) ; son action se limite à la zone colorée en jaune,
les deux bras de fléau \(OR\) et \(OQ\) sont de même longueur et la longueur \(AB\) est notée \(l\),
\(P\) est le milieu de \(AB\) et \(OP = OR\) ,
l'intensité du courant \(I\) est mesurée par un galvanomètre.
Etablir l'expression de l'intensité du champ \(\vec B_{\mathrm{ext}}\) que l'on souhaite mesurer en fonction de \(I\), \(l\) et la masse \(m\) nécessaire pour équilibrer la balance.
Aide simple
La condition d'équilibre traduit l'égalité des moments des forces qui s'exercent sur chacun des fléaux. La première étape consiste donc à analyser l'ensemble des forces de nature magnétostatique et de nature mécanique.
Rappel de cours
Le produit scalaire :
\(\vec A.\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} . \left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =A_1B_1+A_2B_2+A_3B_3\)
Le produit vectoriel :
\(\vec A\wedge\vec B=\left(\begin{array}{c} A_1\\A_2\\A_3\end{array} \right)_{\mathcal{B}} \wedge\left(\begin{array}{c} B_1\\B_2\\B_3\end{array} \right)_{\mathcal{B}} =\left(\begin{array}{c} A_2B_3-A_3B_2\\A_3B_1-A_1B_3\\A_1B_2-A_2B_1\end{array} \right)_{\mathcal{B}}\)
Les opérateurs vectoriels :
Système de repérage cartésien \(\mathcal{B}_{\mathrm{cart.}}(\vec{e_x}, \vec{e_y}, \vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial x} } \\ \displaystyle{ \frac{\partial U}{\partial y} } \\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) | \(\displaystyle{ \frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z} } \\ \displaystyle{ \frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x} } \\ \displaystyle{ \frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y} }\end{array} \right)_{\mathcal{B}_{\mathrm{cart.}}}\) |
Système de repérage cylindrique \(\mathcal B_{\mathrm{cyl.}}(\vec{e_r},\vec{e_{\theta}},\vec{e_z})\)
gradient : \(\vec{\mathrm{grad}}U\) | divergence : \(\mathrm{div}\vec A\) | rotationnel : \(\vec{\mathrm{rot}}\vec A\) |
\(\left(\begin{array}{c} \displaystyle{ \frac{\partial U}{\partial r} } \\ \displaystyle{ \frac{1}{r} \frac{\partial U}{\partial \theta} }\\ \displaystyle{ \frac{\partial U}{\partial z} } \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) | \(\displaystyle{ \frac{1}{r} \frac{\partial (r . A_r) }{\partial r} + \frac{1}{r} \frac{\partial A_{\theta}}{\partial \theta}+\frac{\partial A_z}{\partial z} }\) | \(\left(\begin{array}{c} \displaystyle{ \frac{1}{r} \frac{\partial A_z}{\partial \theta}-\frac{\partial A_ \theta}{\partial z} } \\ \displaystyle{ \frac{\partial A_r}{\partial z}-\frac{\partial A_z}{\partial r} } \\ \displaystyle{ \frac{1}{r} \left( \frac{\partial (r. A_{\theta})}{\partial r}-\frac{\partial A_r}{\partial \theta} \right)} \end{array} \right)_{\mathcal{B}_{\mathrm{cyl.}}}\) |
Nom de l'outil | Comment s'énonce-t-il ? | Quand l'utiliser ? |
Théorème d'Ampère | \(\displaystyle{ \oint_{\mathcal C}\vec B.\vec{\mathrm{d}l}=\mu_0\sum I }\) | Pour calculer \(\vec B\) si la géométrie du problème permet un calcul simple de la circulation de \(\vec B\). |
Loi de Biot et Savart | \(\displaystyle{ \vec B(M)=\frac{\mu_0}{4\pi}\int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\frac{\vec{PM}}{PM^3} }\) | Pour calculer \(\vec B\) si la géométrie de la distribution ne permet pas une application simple du théorème d'Ampère. |
Relation champ magnétostatique/ potentiel vecteur | \(\vec{B}(M)=\vec{\mathrm{rot}}\vec A(M)\) | Pour calculer \(\vec B\) si \(\vec A\) est connu. |
Définition de la force de Laplace | \(\vec{F_m}=\displaystyle{ \int_{\mathcal D}\vec{\mathrm{d} \mathcal C}(P)\wedge\vec B_{\mathrm{ext}}(P) }\) | Pour calculer la force qui s'exerce sur une distribution \(\mathcal D\) soumise à un champ magnétostatique extérieur \(\vec B_{\mathrm{ext}}\) |
Théorème de Maxwell | \(W_{2\leftarrow1}=I . \Phi_c\) | Pour calculer directement le torseur des forces qui agissent sur un circuit. |
Définition du potentiel vecteur | \(\displaystyle{ \vec A(M)=\int_{\mathcal D}\frac{\mu_0}{4\pi}\frac{\vec{\mathrm{d}\mathcal C}(P)}{PM} }\) | Pour calculer \(\vec A\) si la distribution a un haut degré de symétrie. |
Solution détaillée
Examinons tout d'abord les forces qui s'exercent sur la partie de circuit plongée dans le champ magnétostatique.
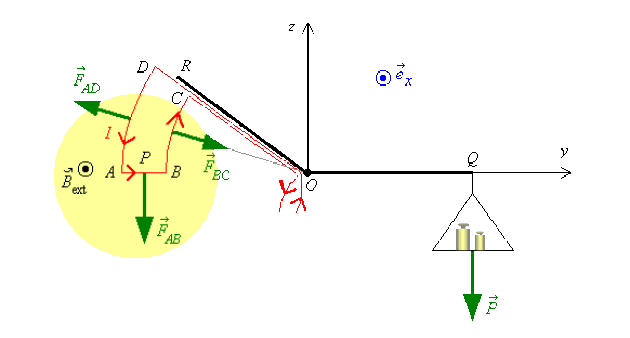
La force de Laplace élémentaire est donnée par \(\vec{\mathrm{d} F} = I \vec{\mathrm{d} l} \wedge \vec B_{\mathrm{ext}}\). Cette relation permet dans un premier temps de trouver la direction et le sens des forces magnétostatiques s'exerçant sur le circuit que l'on décompose en 4 côtés.
- Côtés \(AD\) et \(BC\) : les forces de Laplace sont radiales.
- Côté \(AB\) : la force de Laplace est verticale et dirigée vers le bas. Elle se calcule en intégrant la loi de Laplace sur le tronçon \(AB\) :
\(\vec{\mathrm{d} F}_{AB} = I \vec{\mathrm{d} l} \wedge \vec B_{\mathrm{ext}} = - I . \mathrm{d} l . B_{\mathrm{ext}} . \vec{e_z}\)
d'où la force résultante, appliquée en \(P\) au milieu de \(AB\), \(\displaystyle{F_{AB} = \int_A^B \mathrm{d} F_{AB} = I . l . B_{\mathrm{ext}} }\)
- Côté \(DC\) : la force de Laplace est nulle puisqu'il se trouve en dehors de la zone où s'exerce \(\vec B_{\mathrm{ext}}\).
De l'autre côté de la balance, la masse \(m\) permet l'équilibrage ; le poids \(\vec P\) s'exerce verticalement et vers le bas. Il est donné par \(P = m . \mathrm{g}\).
Calculons les moments de ces forces par rapport au point \(O\).
- Moment du poids : \(\mathcal{M}_P = m . \mathrm{g} . OQ\)
- Moment de la force magnétostatique qui s'exerce sur \(AB\) : \(\mathcal{M}_{F_{AB}} = F_{AB} . OP = I . l . B_{\mathrm{ext}} . OP\)
- Moment des forces magnétostatiques qui s'exercent sur les côtés \(AD\) et \(BC\) : ces forces étant radiales, leur support passe par le point \(O\), d'où un moment par rapport à \(O\) nul. Elles ne sont donc pas à prendre en compte pour écrire la condition d'équilibre de la balance qui fait le bilan des moments par rapport à \(O\).
L'équilibre de la balance se traduit par l'égalité des moments : \(\mathcal{M}_{F_{AB}} = \mathcal{M}_P\)
d'où : \(I . l . B_{\mathrm{ext}} . OP = m . \mathrm{g} . OQ\)
En simplifiant par \(OP\) et \(OQ\) (\(OP = OQ = OR\)), on obtient finalement l'expression du champ que l'on cherche à mesurer : \(\displaystyle{ B_{\mathrm{ext}} = \frac{m . \mathrm{g}}{I . l} }\)