Forces et travail en magnétostatique

Dans le cas d'un régime stationnaire, pour un déplacement fini du circuit filiforme placé dans le champ magnétostatique extérieur \(\stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\), on a, après intégration de l'équation précédente ( \(\mathsf{I}\) est une constante puisque l'on est en régime stationnaire) : \(W = I\Phi_c\)

\(\Phi_c\) étant le flux de \(\stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\) à travers la surface \(\mathfrak{S}_c\) balayée (on dit aussi coupée) par tout le circuit, au cours d'un déplacement déterminé.

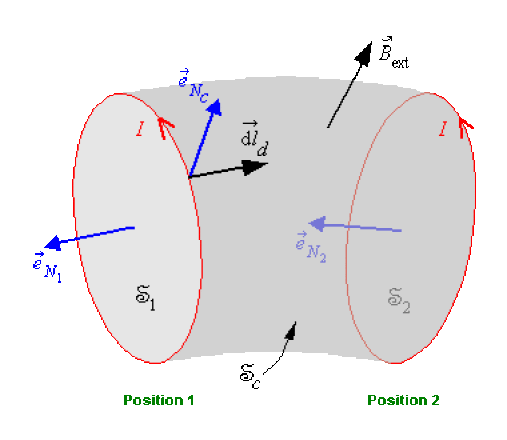
\(\Phi_c\) a un signe lié à l'orientation de la surface coupée \(\mathfrak{S}_c\).

Ce signe découle de l'expression du produit vectoriel \([\overrightarrow{\mathrm{d}l}_d \wedge \overrightarrow{\mathrm{d}l}(P)]\) tel que nous l'avons précisé précédemment, d'où le sens de \(\vec e_{N_c}\) sur la figure précédente.

Comme le flux de \(\stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\) est conservatif, on a :

\(\Phi = \oiint_{\mathfrak{S}}\stackrel{\hookrightarrow}{B_{\mathrm{ext}}} . \overrightarrow{\mathrm{d}\mathfrak{S}} = 0 = \iint_{\mathfrak{S}_1}\stackrel{\hookrightarrow}{B_{\mathrm{ext}}} . \overrightarrow{\mathrm{d}\mathfrak{S}_1} + \iint_{\mathfrak{S}_2}\stackrel{\hookrightarrow}{B_{\mathrm{ext}}} . \overrightarrow{\mathrm{d}\mathfrak{S}_2} + \iint_{\mathfrak{S}_c}\stackrel{\hookrightarrow}{B_{\mathrm{ext}}} . \overrightarrow{\mathrm{d}\mathfrak{S}_c} = 0\)

Où \(\mathfrak{S} = \mathfrak{S}_1 \cup \mathfrak{S}_2 \cup \mathfrak{S}_c\) constitue une surface fermée.

Si \(\Phi_2\) et \(\Phi_1\) représentent les flux de \(\stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\) à travers \(\mathfrak{S}_2\)et \(\mathfrak{S}_1\), c'est-à-dire à travers le circuit dans les positions 2 et 1 (voir schéma), compte tenu également des orientations de \(\mathfrak{S}\), de \(\mathfrak{S}_2\) et \(\mathfrak{S}_1\) liées, pour ces dernières, au sens du courant :

\(\Phi_1 - \Phi_2 + \Phi_c = 0\), ce qui donne : \(\Phi_c = \Phi_2 - \Phi_1\).