Forces et travail en magnétostatique

Considérons un circuit plan, rigide et filiforme \(\mathfrak{D}\), parcouru par un courant d'intensité \(\mathsf{I}\) constante et placé dans un champ magnétostatique extérieur \(\stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\) uniforme.

La force de Laplace à laquelle il est soumis s'écrit :

\(\displaystyle{\vec F_m = \int_{\mathfrak{D}}I\overrightarrow{\mathrm{d}l}(P) \wedge \stackrel{\hookrightarrow}{B_{\mathrm{ext}}} = I \Big[ \int_{\mathfrak{D}} \overrightarrow{\mathrm{d}l}(P)\Big] \wedge \stackrel{\hookrightarrow}{B_{\mathrm{ext}}} = \vec 0}\)

car \(\displaystyle{\int_{\mathfrak{D}} \overrightarrow{\mathrm{d}l}(P) = \vec 0}\).

La résultante des forces de Laplace, qui agit sur un circuit placé dans un champ magnétostatique uniforme, est donc nulle ; ainsi, ce circuit ne subit pas de translation.

S'il se déplace pour obéir à la règle du flux maximum, il ne peut qu'être en rotation autour d'un axe, c'est à dire qu'il est soumis à un couple.

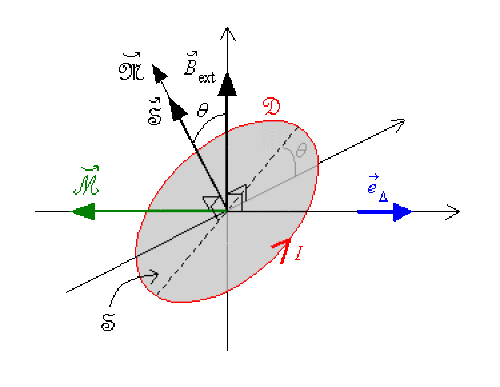
Soit \(\Delta\) cet axe de rotation de vecteur unitaire \(\vec e_{\Delta}\) et \(\vec{\mathfrak{M}} = \mathfrak{M}_{\Delta}\vec e_{\Delta}\) le moment du couple.

Pour une rotation \(\mathrm{d}\theta\) autour de \(\Delta\), le travail des forces a pour expression :

\(\delta W = I \mathrm{d}\Phi = I \mathrm{d}(B_{\mathrm{ext}} \mathfrak{S} \cos\theta) = -I\mathfrak{S}B_{\mathrm{ext}} \sin\theta \mathrm{d}\theta =\mathfrak{M}_{\Delta}\mathrm{d}\theta\)

Ainsi, \(\vec{\mathfrak{M}} = -I \mathfrak{S} B_{\mathrm{ext}} \sin\theta \vec e_{\Delta}\)

Comme le moment magnétique du circuit s'écrit \(\stackrel{\hookrightarrow}{\mathcal{M}} = I \stackrel{\hookrightarrow}{\mathfrak{S}}\), on a \(\stackrel{\hookrightarrow}{\mathfrak{M}} = \stackrel{\hookrightarrow}{\mathcal{M}} \wedge \stackrel{\hookrightarrow}{B_{\mathrm{ext}}}\)