Conclusion
Ce qu'il faut retenir :
En mécanique classique :
La mesure du temps est un invariant par changement de référentiel
La distance instantanée est invariante par changement de référentiel
Si [\(R\)] et [\(R_a\)] sont deux référentiels
La composition des distances additionne les vecteurs :
position de p par rapport à [\(R_a\)] et
position de p par rapport à [\(R\)]
chaque instant, la vitesse par rapport à [\(R_a\)] d'une particule est égale à la somme de la vitesse par rapport à[\(R\)] (en supposant [\(R\)] immobile) de la particule et de la vitesse d'entrainement d'un point de [\(R\)] coincidant avec la particule à cet instant.
\(\displaystyle{\overrightarrow{v(P)}/[R_a]=\overrightarrow{v(P)}/[R]+\overrightarrow{v(P*)}/[R_a]}\)
La vitesse d'entrainement est, dans le cas le plus général, somme d'un terme de translation et d'un terme de rotation

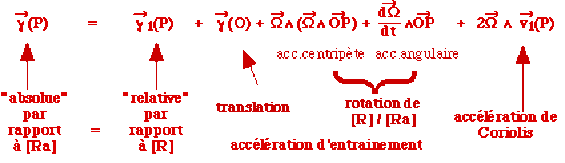
L'accélération d'entrainement est la somme d'une accélération de translation, et d'une accélération de rotation ; cette dernière se décompose en un terme d'accélération angulaire et un terme centripète