Changements d'espace-temps

Le mot "translation" signifie que les vecteurs \(\displaystyle{\vec i,\vec j\textrm{ et }\vec k}\), ont une direction fixe par rapport à \(\displaystyle{\vec u,\vec v,\vec w }\)il n'y a pas de rotation de [\(R_a\)] par rapport à [\(R\)].

Pour simplifier nous prendrons les axes respectivement parallèles entre eux :

\(\displaystyle{\vec i=\vec u\quad\vec j=\vec v\quad\vec k=\vec w}\)

Par suite : \(\displaystyle{\frac{{d}\vec i}{{d}t}=\frac{{d}\vec j}{{d}t}=\frac{{d}\vec k}{{d}t}=0}\)

Donc: \(\displaystyle{(\frac{{d}\vec A}{{d}t})/[R_a]=(\frac{{d}\vec A}{{d}t})/[R]}\)

Cette relation est vérifiée chaque fois qu'il n'y a pas rotation des axes les uns par rapport aux autres; mais le mouvement de l'origine \(O_1\) du repère [\(R\)] peut être quelconque.

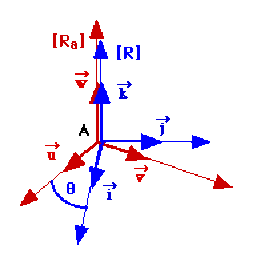
Pour simplifier , on supposera les origines des référentiels confondues ainsi que les vecteurs \(\displaystyle{\vec w\textrm{ et }\vec k}\).

\(\displaystyle{\vec i\textrm{ et }\vec j}\) tournent dans le plan (\(\displaystyle{\vec u,\vec v}\)). On repère la position de [\(R\)] dans [\(R_a\)] par l'angle \(\displaystyle{\theta=(\vec u,\vec i)}\). On remarque que les vecteurs \(\displaystyle{\vec i\textrm{ et }\vec j}\)correspondent aux vecteurs de la base polaire:

\(\displaystyle{\vec i=\vec u_r\textrm{ et }\vec j=\vec u_B}\)

En reportant dans l'expression (3-1) :

\((\frac{d\vec A}{dt})/[R_a]=(\frac{d\vec A}{dt})/[R]-A_y\Omega_e\vec i+A_x\Omega_e\vec j\)

Et par suite: \(\displaystyle{(\frac{{d}\vec A}{dt})/[R_a]=(\frac{{d}\vec A}{{d}t})/[R]+\vec\Omega\land\vec A}\)

En effet: \(\vec\Omega\wedge\vec A=\left|\begin{array}{ccc}\vec i&\vec j&\vec k\\0&0&\Omega\\ A_x&A_y&A_z \end{array}\right|=-A_y\Omega\vec i+A_x\Omega\vec j\)

Soient deux référentiels de même origine, [\(R_a\)] et [\(R\)] , [\(R\)] étant en rotation par rapport à [\(R_a\)] autour d'un axe \(\triangle\) passant par l'origine.

La direction de \(\triangle\), qui peut varier au cours du temps, est repérée par un vecteur \(\vec\Omega=\Omega\;\vec u\) porté par \(\triangle\).

La relation suivante reste valable.

\(\displaystyle{(\frac{{d}\vec A}{{d}t})/[R_a]=(\frac{{d}\vec A}{{d}t})/[R]+\vec\Omega\land\vec A}\)

« La simulation suivante montre la construction des trois composantes du vecteur rotation instantanée lorsque la rotation s'effectue autour d'un axe quelconque variable. »

Remarque

On note quelquefois différemment les opérateurs de dérivation par rapport à chaque référentiel, ce qui permet d'omettre sans risque d'erreur, les indices dans l'écriture:

•  \(\displaystyle{\frac{{d}}{{dt}}}\)est utilisé pour la dérivation temporelle par rapport à un référentiel considéré comme "fixe"

•  \(\displaystyle{\frac{{D}}{{Dt}}}\)est utilisé pour la dérivation temporelle par rapport à un référentiel quelconque, en rotation par rapport au précédent

\(\displaystyle{\frac{{d}\cdot}{{dt}}\overrightarrow A=(\frac{{D}\cdot}{{Dt}}+\overrightarrow\Omega\wedge\cdot)\overrightarrow A=\frac{{d}\overrightarrow A}{{dt}}=(\frac{{D}\overrightarrow A}{{Dt}}+\overrightarrow\Omega\wedge\overrightarrow A)}\)

Si les deux référentiels sont en translation : \(\displaystyle{\frac{{d}}{{dt}}=\frac{{D}}{{Dt}}}\)