Exercice de tir (version western).
Durée : 10 mn
Note maximale : 10
Question
Un jeu très prisé des as de la gâchette consiste à atteindre d'un projectile une cible qu'un acolyte lance en l'air.
La cible est lancée verticalement depuis le sol, au point \(B\), avec une vitesse initiale \(\vec{v_0}\) à l'instant \(t = 0\). Le tireur, posté au niveau du sol au point \(A\), à la distance \(D\) de la cible, est mis au défi de réussir à l'atteindre.
En considérant la cible et le projectile comme des points matériels et en raisonnant par rapport à un référentiel non galiléen que vous choisirez, examinez comment le tireur doit s'y prendre pour relever le défi de la façon la plus simple et la plus efficace.
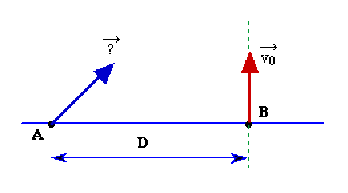
Plus précisément, et si on admet que les forces de frottement avec l'air sont négligeables, utilisez les enseignements de l'exercice précédent pour déterminer à quel instant \(t > 0\) il doit appuyer sur la détente et dans quelle direction il doit viser à ce moment-là.
Montrez que la théorie prévoit qu'il peut aussi réussir s'il choisit d'appuyer sur la détente à l'instant \(t=0\) et déterminez dans quelle direction il doit viser à ce moment là. Expliquez pourquoi cette solution n'est pas la meilleure.
Solution
Il est commode, pour résoudre un problème de visée, de raisonner par rapport au référentiel où la cible est au repos au point \(C\), qu'on appelle aussi le référentiel propre de la cible.
Ce référentiel lié à la cible, n'est pas galiléen. Il est animé, par rapport au référentiel galiléen du tireur (la Terre), d'un mouvement uniformément accéléré (celui de la cible) dont le vecteur accélération est égal à celui de la pesanteur :\(\vec{g}\).
(1 point)
En outre, la vitesse d'entraînement du référentiel propre est égale à \(\vec{v_0}\) à l'instant \(t=0\).
(1 point)
Inversement, les points \(A\) et \(B\) liés à la Terre sont entraînés par rapport au référentiel propre dans un mouvement uniformément accéléré dont le vecteur accélération est égal à \(-\vec{g}\), avec une vitesse initiale \(-\vec{v_0}\), alors que le vecteur \(\vec{AB}\) reste invariant :
\(\vec{AB}(t)=\vec{AB}\).
On a ainsi,
\(\vec{CB}=+\vec{g}\frac{t^2}{2}-\vec{v_0}t\) et \(\vec{CA}=\vec{CB}+\vec{BA}=+\vec{g}\frac{t^2}{2}-\vec{v_0}t-\vec{AB}\)
(1 point)
Le tireur posté au point \(A\) est animé d'un mouvement relatif par rapport à la cible sur une droite verticale passant à la distance \(D\) du point \(C\).
Sur cette droite, la vitesse du tireur \(\vec{v}(t)=+\vec{g}t-\vec{v_0}\) s'annule à l'instant \(T_0=\frac{v_0}{g}>0\) où \(v_0=|\vec{v_0}|\).
lorsque la distance \(CB\) séparant le sol de la cible est maximale.
(1 point)
Si on choisit comme origine des temps l'instant \(T_0\) où la vitesse d'entraînement du tireur est nulle, les conditions initiales sont celles de l'exercice précédent : la cible se trouve à une distance stationnaire du sol, \(h=-g\frac{{T_0}^2}{2}+v_0T_0=\frac{{v_0}^2}{2g}\)
(1 point)
Donc à l'instant \(T_0\) où il s'immobilise par rapport à la cible, il suffit au tireur de la viser pour être certain de l'atteindre quelque part sur la verticale passant par le point \(B\) quelle que soit la valeur initiale de la vitesse \(V_0\) du projectile.
(1 point)
S'il choisit d'appuyer sur la détente à l'instant \(t = 0\), il lui faut faire en sorte que le projectile et la cible se rencontrent quelque part à un instant \(T > 0\).
Or le point \(P\) où se trouve le projectile à un instant \(t > 0\) est déterminée par \(\vec{CP}(t)=-\vec{AB}+(\vec{V_0}-\vec{v_0})t\)
où \(-\vec{v_0}\) est la vitesse avec laquelle le tireur est entraîné par rapport à la cible à l'instant \(t = 0\).
(1 point)
En écrivant que \(P\) et \(C\) sont confondus à l'instant \(T\) de la collision, on trouve
\(\vec{CP}(t)=-\vec{AB}+(\vec{V_0}-\vec{v_0})t=\vec{0}\)
de sorte que la différence de vitesses \(\vec{V_0}-\vec{v_0}\) doit être portée par la droite \(AB\).
(1 point)
Donc, s'il choisit d'appuyer sur la détente à l'instant \(t = 0\), le tireur ne doit pas viser la cible mais pointer son arme dans une direction (qui est celle de ) telle que \(\vec{V_0}-\vec{v_0}\) soit dirigé vers la cible. Il est clair que cette condition ne peut pas être réalisée instantanément par le tireur car il ne maîtrise pas la vitesse \(\vec{v_0}\) de la cible et il ignore en général la vitesse \(V_0\) du projectile.
(1 point)
En revanche, la condition précédente peut faire l'objet d'une vérification expérimentale. Connaissant les vitesses \(V_0\) et \(v_0\), il suffit de viser dans la direction formant avec la droite \(AB\) un angle \(\alpha\) tel que \(\sin\alpha=\frac{v_0}{V_0}\)
L'impact se produira à l'instant \(T\) défini par la relation
\(V_0=\frac{|\vec{AB}+\vec{v_0}T|}{T}\)
(1 point)