Mesure des petites rotations : méthode de Poggendorf [Miroir plan]

Mesure des petites rotations : méthode de Poggendorf

Elle utilise la rotation du rayon réfléchi; pour de petites rotations on peut admettre que le déplacement d'un spot lumineux sur une règle graduée repère avec assez d'exactitude la déviation d'un équipage mobile muni d'un petit miroir plan (dynamomètre, électromètre, galvanomètre).

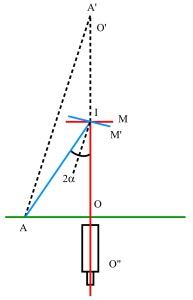
Un miroir plan M donne du trait O d'une règle R parallèle au miroir une image^[1] O'. L'objectif d'un viseur donne de O' jouant le rôle d'objet^[2] une image O'' en coïncidence avec le fil vertical du réticule. Supposons que le miroir tourne d'un angle \(\alpha\) autour de l'axe vertical I et vienne en M'. Nous voyons alors dans le viseur, en coïncidence avec le fil du réticule, le trait A de la règle dont l'image est en A' sur OIO' tel que :

\(\tan(2\alpha)=\frac{\mathrm{OA}}{\mathrm{OI}}\)

Supposons qu'à la limite on puisse apprécier une longueur \(\mathrm{OA}=0,1~\mathrm{mm}\). Soit \(\mathrm{OI}= 1~\mathrm m\). D'où :

\(2\alpha=10^{-4}~\mathrm{radian}~~\) ou encore \(~~\alpha=10''\) environ

Notes

Image
On appelle image d'un objet par un système optique, l'ensemble des images des points de l'objet.
On appelle image d'un point, la zone de convergence des rayons, après traversée du système optique (image réelle) ou la zone d'où les rayons semblent provenir (image virtuelle). Lorsque cette zone se réduit à un point, le système est dit stigmatique.
En pratique, l'image ressemble à l'objet (sinon le système ne présente pas d'intérêt), elle peut être
- agrandie : plus grande que l'objet ( |grandissement| >1) ;
- rapetissée : plus petite que l'objet ( |grandissement| <1) ;
- droite : dans le même sens que l'objet (grandissement >0) ;
- renversée : dans le sens contraire à l'objet (grandissement <0) ;
- déformée : un système qui déforme parce qu'il n'a pas le même grandissement dans différentes directions provoque une anamorphose (ex : glace déformante) ;
- floue
Objet
En optique, on appelle objet tout ensemble de points lumineux. Il peut s'agir d'une source primaire qui produit de la lumière (ex : soleil, étoiles, filament de lampe allumée, écran de télévision ou d'ordinateur en fonction), ou d'une source secondaire qui diffuse une partie de la lumière qu'elle reçoit (ex : lune, planètes, la plupart des objets qui nous entourent lorsqu'ils sont éclairés).
On considère, en général, des objets plans situés dans des plans de front de systèmes optiques.
Dans des systèmes composés on pourra considérer qu'une image produite par une première partie du système est un objet pour le reste du système.