Télescope (2)
Durée : 5 mn
Note maximale : 2
Question
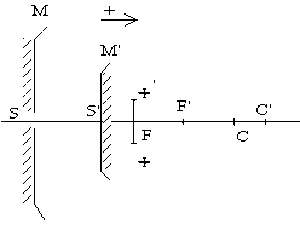
Etude d'un télescope : (suite) on observe cette image en perçant un trou dans \(M\) et en utilisant un petit miroir \(M'\) convexe pour renvoyer les rayons lumineux. On veut que l'image finale soit réelle.
Comment doit on placer \(M'\) et quel est le signe de son grandissement ?
Solution
si l'image est en \(A'\) et que celle-ci doit être réelle on doit avoir :
\(\overline{S'A'}<0\) or \(\frac1{\overline{S'A'}}+\frac1{\overline{S'F}}=\frac2{\overline{S'C'}}=\frac1{\overline{S'F'}}\)
\(\frac1{\overline{S'A'}}=\frac1{\overline{S'F'}}-\frac1{\overline{S'F}}\)
\(\overline{S'A'}=\frac{\overline{S'F}\cdot\overline{S'F'}}{\overline{S'F}-\overline{S'F'}}\)
1er cas : \(\overline{S'F}<0\) et \(\overline{S'F'}>0\) alors \(\overline{S'F}\cdot\overline{S'F'}<0\) et \(\overline{S'F}-\overline{S'F'}<0\) ce qui implique que : \(\overline{S'A'}>0\) ce qui est impossible
2ème cas :\(\overline{S'F}>0\) alors \(\overline{S'F}\cdot\overline{S'F'}<0\) et on doit avoir \(\overline{S'F}-\overline{S'F'}<0\) pour que \(\overline{S'A'}<0\)
soit :
\(\overline{S'F'}>\overline{S'F}\) or \(\gamma=-\frac{\overline{S'A'}}{\overline{S'F}}>0\) \(\gamma>0\) (2 pts)