Télescope (4)
Durée : 5 mn
Note maximale : 2
Question
Etude d'un télescope(suite) : application: f = 5 m, k = 50 ;
calculer \(SS'\) et \(R'\).
Si l'on admet pouvoir distinguer sur la plaque photo deux points distants d'au moins 50 microns, quelle est la limite \(\alpha_0\) au dessous de laquelle l'objet céleste n'est plus vu comme un point ?
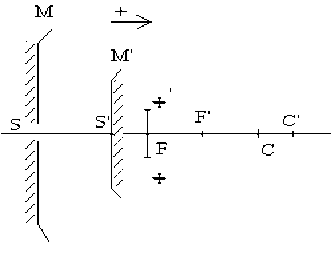
Solution
Alors \(\overline{S'S}=-4,9\textrm m\) et \(R'=0,2\textrm m\) \(\overline{SF'}=\overline{SS'}+\overline{S'F'}=4,9+\frac{0,2}2=5\textrm m\)
\(\gamma=\frac{\overline{A'B'}}{\overline{\Phi\Phi'}}=\frac{\overline{A'B'}}{R.\tan\alpha}=k\) on en déduit : \(\tan\alpha=\frac{\overline{A'B'}}{kR}\)
calculons la valeur limite \(\alpha_0\) correspondant à 2 points \(A'\) et \(B'\) distants de 50 microns :
\(\alpha_0=A\tan\frac{A'B'}{kR}=A\tan\frac{50.10^{-6}}{50.10}=0,1.10^{-6}\) soit : \(2\alpha_0=0,2.10^{-6}\textrm{rad}\).