Construction (2)
Partie
Question
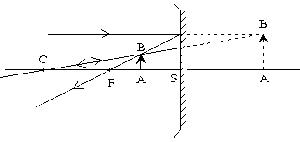
Trouver la position (en m, par rapport au sommet du miroir) et la taille de l'image obtenue (grandissement) dans les conditions de Gauss, de l'objet AB, par construction géométrique, puis par les formules de conjugaison pour un miroir concave de rayon R = 4 m , AB est virtuel, situé à 2 m du sommet.
Utiliser des rayons particuliers
Aide simple
Utiliser deux des trois rayons particuliers suivants :
rayon incident parallèle à l'axe
rayon incident passant par le foyer
rayon incident passant par le centre
pour la construction puis les relations de conjugaison du miroir sphérique.
Rappel de cours
Construction du rayon conjugué
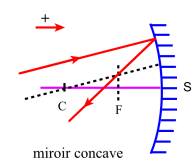
Pour faire une telle construction, il faut se souvenir que :
tout rayon parallèle à l'axe est réfléchi en passant par le foyer
tout rayon passant par le centre optique est réfléchi sur lui-même.
En outre, tout objet ponctuel situé à l'infini a son image dans le plan focal.
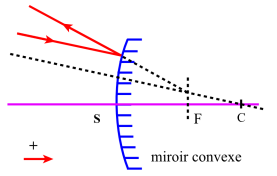
Il en résulte les constructions ci contre dans le cas
d'un miroir concave et
d'un miroir convexe.
Formules de conjugaison
Descartes
si \(p=\overline{SA}\quad p'=\overline{SA'}\quad f=\overline{SF}\) alors :
\(\frac1{p'}+\frac1p=\frac1f\) avec \(\gamma=\frac{\overline{A'B'}}{\overline{AB}}=-\frac{p'}{p}\)
Newton
si \(\delta=\overline{FA}\quad\delta=\overline{FA'}\) et \(f=\overline{SF}=\overline{SF'}=f'\) (attention !) alors :
\(\delta\delta'=f^2\) avec \(\gamma=\frac{\overline{A'B'}}{\overline{AB}}=-\frac{\delta'}f=-\frac f\delta\)