Lentille demi-boule
Durée : 10 mn
Note maximale : 4
Question
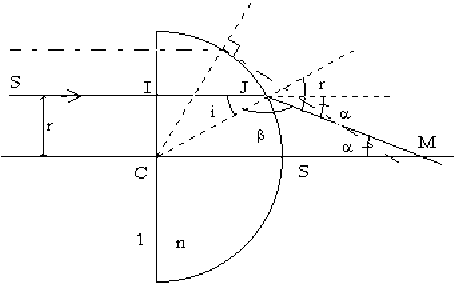
Un faisceau lumineux cylindrique de rayons parallèles tombe sous incidence normale sur la face plane d'une lentille demi-boule de rayon \(R\) et d'indice \(n\), placée dans l'air. (A.N : R = 10 cm ; \(n=\sqrt2\))
Déterminer le point \(M\) où le rayon \(SI\) coupe l'axe après réfraction.
Montrer que quand \(r\) (distance du rayon incident par rapport à l'axe optique) varie de 0 à \(R\), \(M\) décrit un segment \(M_0M_1\) (aberration longitudinale). A quoi correspond l'un des points \(M_0\) ou \(M_1\). Comment peut-on limiter cette aberration?
Solution
\(n \sin i = \sin r\)
il existe un angle limite \(\lambda\) tel que :
\(n\sin\lambda=1\)
\(\sin\lambda=\frac1n\)
Dans le triangle \(CJM\) on a : \(\frac{\sin\beta}{CM}=\frac{\sin\alpha}{CJ}\)
\(CM=\frac{\sin\beta}{\sin\alpha}\cdot CJ=R\cdot\frac{\sin\beta}{\sin\alpha}\)
\(\beta=\pi-i-\alpha=\pi-i-(r-i)=\pi-r\)
puisque \(\alpha=r-i\) d'où
\(CM=R\cdot\frac{\sin(\pi-r)}{\sin(r-i)}=\frac{R.\sin r}{\sin(r-i)}=\frac{nR.\sin i}{\sin r.\cos i-\sin i.\cos r}\)
\(CM=\frac{nR.\sin i}{n.\sin i.\cos i-\sin i.\sqrt{1-n^2\sin^2i}}=\frac{nR}{n.\cos i-\sqrt{1-n^2\sin^2i}}\) (2 pts)
si \(i=0\) alors \(CM_0=\frac{nR}{n-1}=\frac{\sqrt2.R}{\sqrt2-1}\)
si \(i=\lambda\) alors \(CM_\lambda=\frac{n.R}{n.\cos i}=\frac R{\cos i}\)
puisque \(1-n^2\sin^2i=1-n^2\sin^2\lambda=0\)
\(CM_\lambda=\frac R{\sqrt{1-\sin^2\lambda}}=\sqrt2.R\)
\(M_\lambda M_0=\sqrt2.R-\frac{\sqrt2.R}{\sqrt2-1}=R\sqrt2\left(1-\frac1{\sqrt2-1}\right)\)
\(M_\lambda M_0=R\sqrt2\frac{\sqrt2-2}{\sqrt2-1}\)
ce qui correspond à une tache de 20 cm. On peut diminuer cette aberration longitudinale en diminuant \(r\). ( 2 pts)