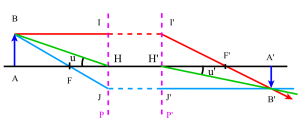
Origine aux foyers
Posons :
\(\overline{\mathrm{FA}}=\mathrm x~\) et \(~\overline{\mathrm{F'A'}}=\mathrm{x'}\)
Les triangles semblables :
FAB et FHJ d'une part,
F'H'I' et F'A'B' d'autre part permettent d'écrire :
\(\frac{\overline{\mathrm{HJ}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{FH}}}{\overline{\mathrm{FA}}}=-\frac{\mathrm f}{\mathrm x}\)
\(\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{H'I'}}}=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{F'A'}}}{\overline{\mathrm{F'H'}}}=-\frac{\mathrm{x'}}{\mathrm{f'}}\)
soit :
\(\frac{\mathrm f}{\mathrm x}=\frac{\mathrm{x'}}{\mathrm{f'}}\)
d'où :
Formules de conjugaison de Newton :
\(\mathrm x.\mathrm{x'}=\mathrm f.\mathrm{f'}\)
\(\gamma=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=-\frac{\mathrm f}{\mathrm x}=-\frac{\mathrm{x'}}{\mathrm{f'}}\)
Définition : Grandissement angulaire
On définit le grandissement angulaire par :
\(\mathrm G=\frac{\mathrm{u'}}{\mathrm u}=\frac{\mathrm n}{\mathrm{n'}}~\frac{\overline{\mathrm{AB}}}{\overline{\mathrm{A'B'}}}\)
On constate que le produit du grandissement linéaire par le grandissement angulaire :
\(\gamma.\mathrm G=\frac{\mathrm n}{\mathrm{n'}}\)
est une constante.