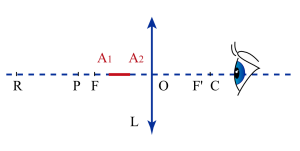
Latitude de mise au point
Pour que l'image \(A'B'\) puisse être vue nettement par l’œil elle doit être située entre le punctum proximum \(P\) et le punctum remotum \(R.\) L'objet [1]ne pourra donc se déplacer qu'entre deux positions \(A_{1}\) et \(A_{2}\) qui sont respectivement les conjugués [2]de \(R\) et \(P.\)
La distance \(A_{1}A_{2}\) est la latitude d'accommodation de l’œil visant à travers la loupe.
Appelons \(d\) et \(D\) les distances minimale et maximale de vision distincte. On a alors :
\(\overline{F'C}=a~~\) \(~~\overline{RC}=D~~\) \(\overline{PC}=d~~\)
\(\overline{FA_{\mathit1}}~.~\overline{FR}=-f'^2~\) soit \(\overline{FA_{\mathit1}}=\frac{f'^2}{D~-~a}\)
\(\overline{FA_{\mathit2}}~.~\overline{FP}=-f'^2~\) soit \(\overline{FA_{\mathit2}}=\frac{f'^2}{d~-~a}\)
et \(\overline{A_{\mathit1}A_{\mathit2}}=\overline{FA_{\mathit2}}~-~\overline{FA_{\mathit1}}=f'^2\Big(\frac1{d~-~a}-\frac1{D~-~a}\Big)\)
\(a\) est de l'ordre de quelques mm et est négligeable devant \(d\) et \(D\)
soit : \(~\overline{A_{\mathit1}A_{\mathit2}}=f'^2\Big(\frac1d-\frac1D\Big)=A.f'^2\)
\(A\) est appelée amplitude dioptrique d'accommodation. Pour l'oeil emmétrope, \(D\) est infini et \(A_{1}\) est en \(F\) d'où : \(~\overline{A_{\mathit1}A_{\mathit2}}=\frac{f'^2}d\). Pour une focale [3] \(f '=6\) cm et une distance minimale de vision distincte égale à \(d=15\) cm il vient : \(FA_{2} = \textrm{2,4 cm}\)