Puissance
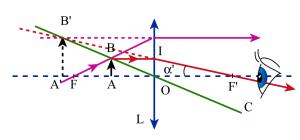
La dimension d'une image [1]rétinienne ne dépend que du diamètre apparent sous lequel est vu l'objet[2]. Si l’œil observe par l'intermédiaire d'une loupe c'est l'image A'B' qu'il regarde. Nous prendrons un objet AB de longueur unité. L'efficacité de la loupe est caractérisée par l'angle \(\alpha'\) sous lequel est vue l'image correspondante A'B'.
Or on a : \(\tan~\alpha'=\frac{A'B'}{A'C}=\frac{A'B'}{AB}~\frac{AB}{A'C}\) en utilisant la formule de Newton en module, on obtient :
\(\frac{A'B'}{AB}=\frac{A'F'}{f'}\)
d'où \(\tan~\alpha'=\frac{A'F'}{f'}~\frac{AB}{A'C}\)
et en posant : \(A'C=\delta\)
qui représente la distance de visée. En appelant P l'angle sous lequel est vue l'unité de longueur de l'objet AB à travers la loupe on peut écrire :
\(P=\frac{\alpha'}{AB}=\frac{A'F'}{f'}~\frac1{\delta}\)
\(P=\frac1{f'}~\Big(1~-~\frac a{\delta}\Big)\)
P représente la puissance [3]de la loupe et un objet [2]de longueur l sera vu sous un angle : \(\alpha'=P.l\)
Si l'oeil est placé au foyer objet [4]de la loupe alors a = 0 et la puissance prend une valeur indépendante de l'observateur que l'on appelle puissance intrinsèque : \(P_i=\frac1{f'}\) qui est égale à la vergence [3]de la loupe. P et \(P_i\) s'expriment en dioptries.
Pour éviter la fatigue due à l'accommodation l'observateur forme l'image au punctum remotum de telle sorte que même si le centre optique [5]de l’œil n'est pas en F', le terme en \(\frac a{\delta}\) est toujours petit devant 1 et on admettra que : la puissance d'une loupe est pratiquement égale à sa convergence \(\frac1{f'}\).