Orientation de l'espace et du plan
Soit un repère orthonormé \(\Big(O,\vec{i},\vec{j},\vec{k}\Big)\) de l'espace.
Notons : \(\vec{i} = \overrightarrow{OA},~ \vec{j} = \overrightarrow{OB} ,~ \vec{k} = \overrightarrow{OC}\)
Orienter l'espace, c'est distinguer les repères "directs" de ceux qui ne le sont pas et nommés "indirects". Certaines règles permettent de les différencier.
\(\qquad\)
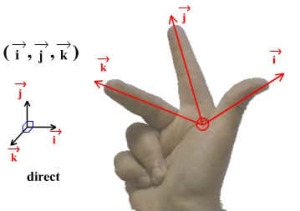
"Règles des trois doigts" de la main droite.
On associe les vecteurs de base \(\Big(\vec{i},\vec{j},\vec{k} \Big)\) aux axes d'un trièdre rectangle formé par les trois doigts de la main droite :
\(\vec{i}\) dans la direction du pouce.
\(\vec{j}\) dans la direction de l'index.
\(\vec{k}\) dans la direction du majeur.
pour former un trièdre direct.
\(\qquad\)
"Règle du bonhomme d'Ampère"
Le trièdre \(\Big(\vec{i},\vec{j},\vec{k} \Big)\) est direct (respectivement indirect) si un homme, traversé par le vecteur \(\overrightarrow{OC}\) des pieds à la tête, regardant \(\overrightarrow{OA}\) a le vecteur \(\overrightarrow{OB}\) à sa gauche (respectivement à sa droite).
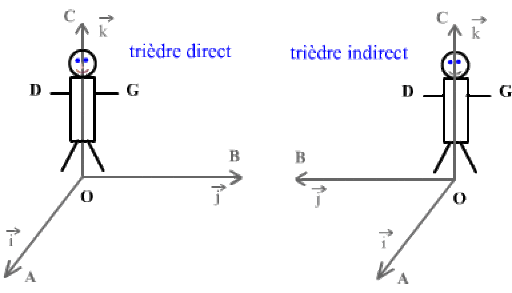
\(\qquad\)
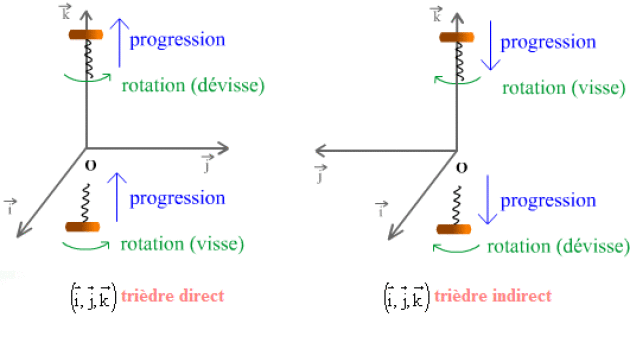
"Règle du tire-bouchon"
Un tire-bouchon que l'on tourne dans le sens qui amène le vecteur \(\vec{i}\) sur le vecteur \(\vec{j}\), progresse dans le sens \(\vec{k}\) si le trièdre \(\Big(\vec{i},\vec{j},\vec{k} \Big)\) est direct (sens \(- \vec{k}\) de si le trièdre est indirect).
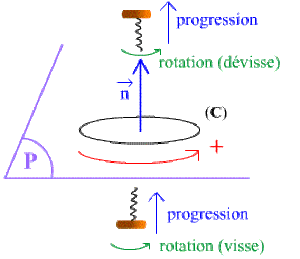
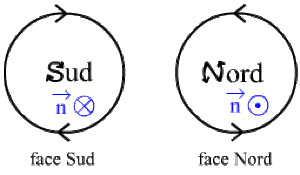
Soit un cercle \((C)\) d'un plan \((P)\) parcouru arbitrairement dans un sens que nous prendrons positif.
Le sens de progression d'un tire-bouchon tournant dans le sens positif progresse dans le sens du vecteur \(\vec{n}\) normal à \((P)\).
Orienter le plan c'est fixer :
soit le sens positif et imposer \(\vec{n}\)
soit \(\vec{n}\) et orienter le sens de parcours.
Le sens de parcours est différent quand le cercle \((C)\) est vu au-dessous de \((P)\) (sens inverse du sens trigonométrique- face Sud) ou au-dessus de \((P)\) (sens trigonométrique - face Nord.)