Applications
En géométrie (dans un repère orthonormé)
Module d'un vecteur \(\overrightarrow{V} \Big(V_{x},V_{y},V_{z}\Big)\)
On a : \(\overrightarrow{V} \cdot \overrightarrow{V} = V_{x}^{2} + V_{y}^{2} + V_{z}^{2} \Rightarrow \Arrowvert \overrightarrow{V} \Arrowvert = \sqrt{V_{x}^{2} + V_{y}^{2} + V_{z}^{2}}\)
Exemple :
Module du vecteur \(\overrightarrow{V}\Big(2,-3,6 \Big)\)
Par définition de \(\overrightarrow{V} \Big(V_{x},V_{y},V_{z}\Big)\), nous avons la norme de \(\overrightarrow{V}\):
\(\begin{array}{ll}\Arrowvert \overrightarrow{V} \Arrowvert & = \sqrt{V_{x}^{2} + V_{y}^{2} + V_{z}^{2}} \\ & = \sqrt{2^{2} + (-3)^{2} + (6)^{2}} \\ &=\sqrt{4+9+36} \\ &= \sqrt{49} = 7 \end{array}\)
Distance entre deux points \(M(x,y,z)\) et \(N(x',y',z')\)
\(d(M,N) = MN = \sqrt{(x'-x)^{2} + (y'-y)^{2} + (z' - z)^{2}}\)
Exemple :
Distance entre les points \(M(-2,1,3)\) et \(N(1,4,-2)\)
Par définition :
\(\begin{array}{ll} d(M,N) & = MN \\ & = \sqrt{(1-(-2))^{2} + (4-1)^{2} + (-2-3)^{2}} \\ &=\sqrt{9+9+25} \\ &= \sqrt{43}\end{array}\)
Détermination du cosinus de l'angle entre deux vecteurs \(\overrightarrow{U}\Big(U_{x},U_{y},U_{z} \Big)\) et \(\overrightarrow{V}\Big(V_{x},V_{y},V_{z} \Big)\)
Par application du produit scalaire :
\(\cos\Big(\overrightarrow{U} , \overrightarrow{V}\Big) = \frac{\overrightarrow{U} \cdot \overrightarrow{V}}{\Arrowvert\overrightarrow{U}\Arrowvert~\Arrowvert\overrightarrow{V}\Arrowvert} = \frac{U_{x}V_{x} +U_{y}V_{y} + U_{z}V_{z}}{\sqrt{U_{x}^{2} + U_{y}^{2} + U_{z}^{2}} \sqrt{V_{x}^{2} + V_{y}^{2} + V_{z}^{2}}}\)
Exemple :
Détermination du cosinus de l'angle entre les vecteurs \(\overrightarrow{U}\Big(0,-3,-3 \Big)\) et \(\overrightarrow{V}\Big(1,-2,-1 \Big)\)
Par application du produit scalaire : \(\cos\Big(\overrightarrow{U} , \overrightarrow{V}\Big) = \frac{\overrightarrow{U} \cdot \overrightarrow{V}}{\Arrowvert\overrightarrow{U}\Arrowvert~\Arrowvert\overrightarrow{V}\Arrowvert}\)
or
\(\overrightarrow{U} \cdot \overrightarrow{V} = \Big(0\Big) \Big(1\Big) + \Big(-3\Big)\Big(-2\Big) + \Big(-3\Big)\Big(-1\Big) = 9\)
\(\Arrowvert\overrightarrow{U}\Arrowvert = \sqrt{(-3)^{2} + (-3)^{2}} = \sqrt{18} = 3 \sqrt{2}\)
\(\Arrowvert\overrightarrow{V}\Arrowvert = \sqrt{1^{2} + (-2)^{2} + (-1)^{2}} = \sqrt{6}\)
d'où \(\cos\Big(\overrightarrow{U} , \overrightarrow{V}\Big) = \frac{9}{3\sqrt{2}\sqrt{6}} = \frac{3}{2\sqrt{3}} = \frac{\sqrt{3}}{2}\)
Relation métrique dans un triangle quelconque
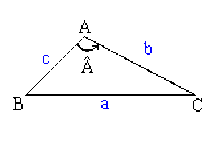
Nous avons \(\overrightarrow{BC} = \overrightarrow{BA} + \overrightarrow{AC}\) d'où
\(\begin{array}{ll}{\overrightarrow{BC}}^{2} &= \Big(\overrightarrow{BA} + \overrightarrow{AC} \Big) \cdot \Big(\overrightarrow{BA} + \overrightarrow{AC} \Big) \\ &={\overrightarrow{BA}}^{2} + {\overrightarrow{AC}}^{2} + 2\overrightarrow{BA} \cdot \overrightarrow{AC} \\ &={\overrightarrow{BA}}^{2} + {\overrightarrow{AC}}^{2} - 2\overrightarrow{AB}\cdot \overrightarrow{AC} \end{array}\)
donc \(a^{2} = b^{2} + c^{2} - 2bc \cdot \cos \hat{A}\)
Exemple :
Déterminer l'angle intérieur à un sommet d'un triangle
On considère un triangle de sommets \(A(-4,-2,0)\) ; \(B(-1,-2,4)\) et \(C(9,-2,-1)\) dans un repère orthonormé. Déterminer l'angle intérieur au sommet \(A\).
Relation du triangle :
\(a^{2} = b^{2} + c^{2} - 2bc ~\cos \hat{A} \Rightarrow \cos \hat{A} = \frac{b^{2} + c^{2} - a^{2}}{2bc}\)
avec
\(\overrightarrow{b} = \overrightarrow{AC} = \overrightarrow{OC} - \overrightarrow{OA} = \left| \begin{array}{c} 9 \\ -2 \\ -1 \end{array} \right. - \left| \begin{array}{c} -4 \\ -2 \\ 0 \end{array} \right. = \left| \begin{array}{c} 13 \\ 0 \\ -1 \end{array} \right. \Rightarrow b^{2} = 13^{2} + 1^{2} = 170\)
\(\overrightarrow{c} = \overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = \left| \begin{array}{c} -1 \\ -2 \\ 4 \end{array} \right. - \left| \begin{array}{c} -4 \\ -2 \\ 0 \end{array} \right. = \left| \begin{array}{c} 3 \\ 0 \\ 4 \end{array} \right. \Rightarrow c^{2} = 3^{2} + 4^{2} = 25\)
\(\overrightarrow{a} = \overrightarrow{BC} = \overrightarrow{OC} - \overrightarrow{OB} = \left| \begin{array}{c} 9 \\ -2 \\ -1 \end{array} \right. - \left| \begin{array}{c} -1 \\ -2 \\ 4 \end{array} \right. = \left| \begin{array}{c} 10 \\ 0 \\ -5 \end{array} \right. \Rightarrow a^{2} = 10^{2} + (-5)^{2} = 125\)
d'où
\(\cos \hat{A} = \frac{170 + 25 - 125}{2\sqrt{170} \times 5} = \frac{7}{\sqrt{170}} \Rightarrow \hat{A} \# \frac{\pi}{3} ~\Big(57^{\circ}53\Big)\)
En Physique
Travail élémentaire \(dW\) d'une force \(\overrightarrow{F}\) constante dont le point d'application se déplace de \(\overrightarrow{dl}\): \(dW = \overrightarrow{F}~ .~ \overrightarrow{dl}\)
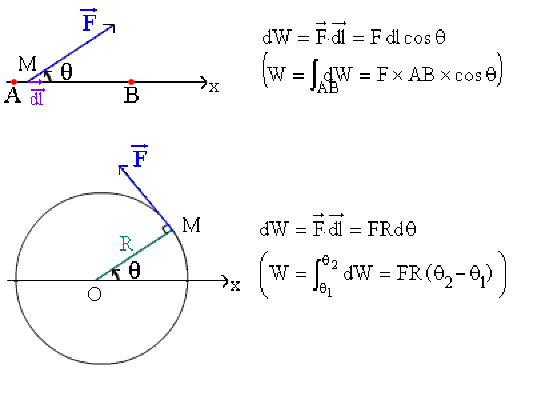
\(\qquad\)
Flux à travers une surface : \(d \phi = \overrightarrow{V}(M) . \overrightarrow{dS}\)
L'intensité d'un courant à travers une section \((S)\) d'un conducteur est le flux du vecteur densité de courant \(\overrightarrow{j}\) à travers \((S)\). Les charges mobiles, de densité volumique \(\rho\), se déplacent à la vitesse \(\overrightarrow{v}\) à travers une surface \(dS\). Pendant le temps \(dt\), la charge traversée sera : \(dq = \rho \overrightarrow{v} dt~ .~ \overrightarrow{dS}\)
En posant \(\overrightarrow{j} = \rho \overrightarrow{v}\) le vecteur densité de courant, nous avons
\(i = \frac{dq}{dt} = \overrightarrow{j} ~. ~\overrightarrow{dS} \Bigg(I = \frac{dQ}{dt} = \iint_{s} \overrightarrow{j} ~. ~\overrightarrow{dS} \Bigg)\)