Question 1
Durée : 5 mn
Note maximale : 6
Question
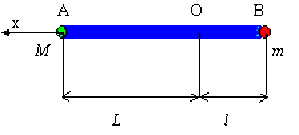
Deux masses \(M\) et \(m\) sont fixées en \(A\) et \(B\) sur une tige \(AB\) de masse négligeable aux distances \(OA = L\) et \(OB = l\) d'un point origine quelconque, de part et d'autre de ce point.
Déterminer la position du centre d'inertie \(G\) du système ( tige et masses \(m\) et \(M\)).
Solution
Le centre d'inertie \(G\) d'un système matériel est défini par :
\(OG \displaystyle{\sum_{i}m_{i} = \sum_{i}m_{i}OA_{i}}\) d'où \((M+m)\overrightarrow{OG} = M~\overrightarrow{OA} + m ~\overrightarrow{OB}\) ( 2 points )
La projection sur l'axe orienté \(\overrightarrow{Ox}\) conduit à :
\((M+m) \overline{OG} = M~\overline{OA} + m ~\overline{OB} = ML - ml \Rightarrow \overline{OG} = \frac{ML - ml}{M+m}\) ( 4 points )