Question 2
Durée : 5 mn
Note maximale : 8
Question
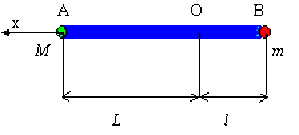
Dans le cas où la tige est homogène de masse \(m'\), définir la nouvelle position du centre d'inertie \(G '\).
Solution
On doit considérer en plus la barre homogène dont le centre d'inertie est \(I\) milieu de \(AB\), affecté de la masse \(m'\).
\((M+m+m') ~\overrightarrow{OG'} = M ~\overrightarrow{OA} + m ~\overrightarrow{OB} + m' ~\overrightarrow{OI}\) ( 2 points )
La projection sur l'axe orienté \(\overrightarrow{Ox}\) conduit à :
\(\overline{OI} = \overline{OA} + \overline{AI} = L + \frac{(-L-l)}{2} = \frac{L-l}{2}\)
d'où
\(\begin{array}{ll}(M+m+m') \overline{OG'} &= M \overline{OA} + m \overline{OB} + m' \overline{OI} \\\\& = ML - ml + m' \frac{L-l}{2} \\\\& =\frac{(2M + m')L - (2m + m')l}{2} \end{array}\)
donc
\(\overline{OG'} = \frac{(2M + m')L - (2m + m')l}{2(M+m+m')}\) ( 6 points )