Question 1
Durée : 5 mn
Note maximale : 6
Question
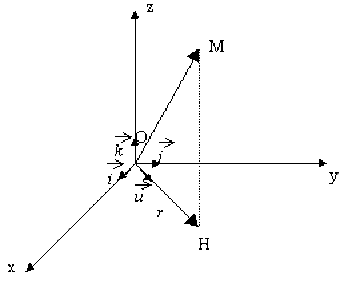
On considère un point matériel \(M\) de masse \(m\) tournant à la vitesse angulaire \(\overrightarrow{\omega} = \omega ~ \vec{k}\) autour d'un axe \(Oz\). Le point \(M\) se projette en \(H\) dans le plan \(xOy\) et on appelle \(\overrightarrow{u}\) le vecteur unitaire porté par \(\overrightarrow{OH}\). On pose \(OH = r\).
Exprimer le vecteur vitesse \(\overrightarrow{v} = \overrightarrow{MO} \wedge \overrightarrow{\omega}\) en fonction de \(\omega\) et \(r\) et des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{k}\).
Solution
Dans l'expression de la vitesse \(\overrightarrow{v} = \overrightarrow{MO} \wedge \overrightarrow{\omega}\) remplaçons les vecteurs \(\overrightarrow{MO}\) et \(\overrightarrow{\omega}\) par
\(\overrightarrow{MO} = \overrightarrow{MH} + \overrightarrow{HO} = -z ~\vec{k} - r ~\vec{u}\) ( 2 points ) et \(\overrightarrow{\omega} = \omega ~\vec{k}\)
d'où :
\(\begin{array}{ll}\overrightarrow{v} &= - \left(z~\vec{k} + r~\vec{u} \right) \wedge \omega ~\vec{k} \\ &= -z ~\omega ~\vec{k} \wedge \vec{k} - r \omega \left(\overrightarrow{u} \wedge \vec{k} \right)\end{array}\)
\(\overrightarrow{v} = - r \omega \left(\overrightarrow{u} \wedge \vec{k} \right)\) ( 4 points )