Question 2
Durée : 7 mn
Note maximale : 14
Question
Calculer en fonction de \(m\), \(r\), \(\omega\) , \(z\), \(\overrightarrow{u}\) et \(\vec{k}\) le moment cinétique \(\overrightarrow{L_0}\) en \(O\), du point matériel \(M\) animé de la vitesse \(\overrightarrow{v}\).
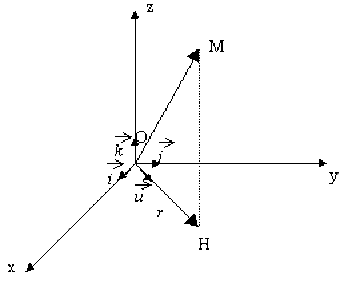
Solution
Par définition, le moment cinétique en \(O\) du point \(M\) est :
\(\begin{array}{ll}\overrightarrow{L_{0}} & = \overrightarrow{OM} \wedge \overrightarrow{p} \\ & = \overrightarrow{OM} \wedge m \overrightarrow{v} \end{array}\) ( 2 points )
\(\begin{array}{ll}&=\left(\overrightarrow{OH} + \overrightarrow{HM}\right) \wedge m \left(- r \omega \left(\overrightarrow{u} \wedge \overrightarrow{k}\right)\right) \\ & = -mr~\omega \left[\left(r \overrightarrow{u} + z \overrightarrow{k} \right) \wedge \left(\overrightarrow{u} \wedge \overrightarrow{k} \right)\right] \end{array}\)
\(\begin{array}{ll} &= -mr~\omega \left[r \overrightarrow{u} \wedge \left( \overrightarrow{u} \wedge \overrightarrow{k} \right) + z\overrightarrow{k}\wedge \left(\overrightarrow{u} \wedge \overrightarrow{k} \right)\right] \end{array}\) ( 4 points )
( D'après la distributivité de la multiplication vectorielle par rapport à l'addition vectorielle).
La définition du double produit vectoriel : \(\overrightarrow{A} \wedge \left(\overrightarrow{B} \wedge \overrightarrow{C}\right) = \left(\overrightarrow{A} \cdot \overrightarrow{C}\right) \overrightarrow{B} - \left(\overrightarrow{A} \cdot \overrightarrow{B} \right)\overrightarrow{C}\) conduit à
\(\overrightarrow{u} \wedge \left(\overrightarrow{u} \wedge \overrightarrow{k}\right) = \left(\overrightarrow{u} \cdot \overrightarrow{k}\right) \overrightarrow{u} - \left(\overrightarrow{u} \cdot \overrightarrow{u} \right)\overrightarrow{k} = - \overrightarrow{k}\) ( 2 points )
\(\overrightarrow{k} \wedge \left(\overrightarrow{u} \wedge \overrightarrow{k}\right) = \left(\overrightarrow{k} \cdot \overrightarrow{k}\right) \overrightarrow{u} - \left(\overrightarrow{k} \cdot \overrightarrow{u} \right)\overrightarrow{k} = \overrightarrow{u}\) ( 2 points )
donc
\(\overrightarrow{L_{0}} = - mr ~\omega \left(-r \overrightarrow{k} + z \overrightarrow{u} \right)\)
\(\overrightarrow{L_{0}} = mr^{2} \omega \overrightarrow{k} - mrz ~\omega \overrightarrow{u}\) ( 4 points )