Question 1
Durée : 5 mn
Note maximale : 6
Question
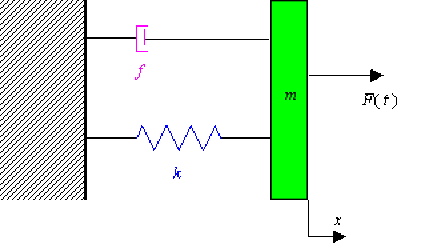
Une force \(F(t) = F_{m} \cos \omega t\) est appliquée à la masse \(m\) , d'un système mécanique (figure), \(f\) coefficient de frottement visqueux et \(k\) constante de raideur du ressort.
Le principe fondamental de la dynamique conduit à l'équation différentielle :
\(m ~x''(t) + f x'(t) + k x(t) = F_{m} \cos \omega t\)
En prenant, comme grandeur de réponse le déplacement \(x(t)\) sous la forme
\(x(t) = x_{m} \cos \left(\omega t + \varphi\right) = \Re\left\{\underline{x}(t)\right\}\) avec \(\underline{x}(t) = \underline{x}_{m} e^{j \omega t}\) où \(\underline{x}_{m} = x_{m} e^{j \varphi}\) déterminer par l'utilisation des complexes : amplitude \(x_m\) et phase \(\varphi\) .
Solution
En utilisant la formulation complexe nous obtenons :
\(x(t) = x_{m} \cos\left(\omega t + \varphi\right) = \Re \left\{\underline{x}(t)\right\}\) où \(\underline{x}(t) = x_{m} e^{\left(j \omega t + \varphi\right)} = \underline{x}_{m} e^{j \omega t}\) avec \(\underline{x}_{m} = x_{m} e^{j \varphi}\) d'où
\(\underline{x}'(t) = j \omega \underline{x}(t)\) et \(\underline{x}'(t) = - \omega^{2} \underline{x}(t)\)
En posant \(F_{m} \cos \omega t = \Re \left\{\underline{F}_{m} e^{j \omega t}\right\}\) avec \(\underline{F}_{m} = F_{m}\)
nous avons :
\(m x''(t) + f x'(t) + k x(t) = \left[\left(-m \omega^{2} + k \right) + jf \omega \right] \underline{x}_{m}(t) = \underline{F}_{m}\)
d'où
\(\underline{x}_{m} = \frac{\underline{F}_{m}}{\left(k-m \omega^{2}\right) + j f \omega} \Rightarrow x_{m} = \frac{F_{m}}{\left[\left(k-m \omega^{2}\right)^{2} + f^{2}\omega^{2}\right]^{1/2}}\) ( 3 points )
et
\(\arg\left(\underline{x}_{m}\right) = \arg \left(\underline{F}_{m}\right)-\arg\left[\left(k-m \omega^{2}\right) + j f \omega \right]\Rightarrow \varphi = -\textrm{Arctan} \left(\frac{f \omega}{k - m \omega^{2}}\right)\) ( 3 points )