Question 1
Durée : 5 mn
Note maximale : 4
Question
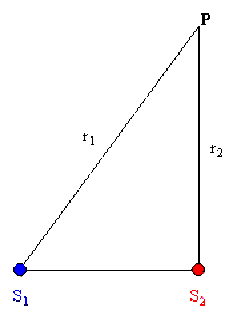
Les sources \(S_1\) et \(S_2\) des ondes acoustiques sphériques dans un milieu homogène et isotrope. Au point \(P\) les vibrations de \(S_1\) et \(S_2\) :
\(\underline{G}_{1} \left(r,t\right) = \frac{A_{1}}{r_{1}} e^{j\left(\omega t - \omega \frac{r_{1}}{v} + \varphi_{1}\right)}\) et \(\underline{G}_{2} \left(r,t\right) = \frac{A_{2}}{r_{2}} e^{j\left(\omega t - \omega \frac{r_{2}}{v} + \varphi_{2}\right)}\)
Déterminer l'amplitude complexe au point \(P\) :\( \underline{G}_{m} = \underline{G}_{1m} + \underline{G}_{2 m}\)
(on pose \(\underline{G}\left(r,t\right) = \underline{G}_{m} \left(r\right) e^{j \omega t}\) )
Solution
L'amplitude complexe a pour expression :
\(\underline{G}_{m} = \underline{G}_{1 m} + \underline{G}_{2 m} = \frac{A_{1}}{r_{1}} e^{j\left(\omega t - \omega \frac{r_{1}}{v} + \varphi_{1}\right)} +\frac{A_{2}}{r_{2}} e^{j\left(\omega t - \omega \frac{r_{2}}{v} + \varphi_{2}\right)} = a_{1} e^{j \theta_{1}} + a_{2} e^{j \theta_{2}}\) ( 4 points )
avec \(a_{1} = \frac{A_{1}}{r_{1}}\), \(a_{2} = \frac{A_{2}}{r_{2}}\) , \(\theta_{1} = \left(- \frac{\omega r_{1}}{v} + \varphi_{1}\right)\) et \(\theta_{2} = \left(- \frac{\omega r_{2}}{v} + \varphi_{2}\right)\)