Question 1
Durée : 6 mn
Note maximale : 8
Question
En régime permanent sinusoïdal, on définit la fonction de transfert d'un circuit par le rapport complexe : \(\underline{H}(j \omega) =\underline{S}/\underline{E} \)où \(\underline{E}\) et \(\underline{S}\) sont respectivement les amplitudes complexes de l'excitation \(e(t)\) à l'entrée et du signal \(s(t)\) à la sortie du réseau.
Les diagrammes de Bode représentent, en fonction de \(\omega\) ( ou de \(\log \omega\) ), le module et l'argument de \(\underline{H} (j \omega)\) :
\(H_{\textrm{db}} = 20 \log \arrowvert\underline{H}\arrowvert\) (exprimé en décibel : \(\textrm{dB}\)) ; \(\arg[\underline{H}]\)
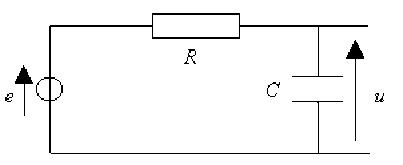
Dans le cas d'une cellule \(RC\), passe bas:
Calculer la fonction de transfert : \(\underline{H} (j \omega) = \underline{U}/\underline{E}\).
Solution
D'après la loi d'Ohm, en notation complexe nous avons :
\(\underline{U} =\underline{Z_{c}} \underline{I} = \frac{1}{j C \omega}\underline{I}\) ( 2 points )
\(\underline{E} = \left(\underline{Z_{R}} + \underline{Z_{C}}\right)\underline{I} = \left(R + \frac{1}{jC \omega}\right)\underline{I}\) ( 2 points )
D'où la fonction de transfert:
\(\underline{H}(j \omega) = \frac{\underline{U}}{\underline{E}} = \frac{\left(1/jC\omega\right)\underline{I}}{\left(R + 1/jC\omega\right)\underline{I}} = \frac{1}{1+jRC\omega}\) ( 4 points )