Notions de base de la trigonométrie circulaire
Mesures des angles
Trois unités sont utilisées pour la mesure d'un angle \(\alpha\) :
le radian \((\textrm{rd})\)
le degré \((^{\circ})\)
le grade \((\textrm{gr})\)
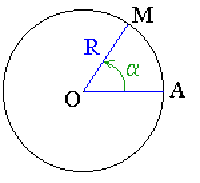
Pour un angle au centre \(\widehat{AOM}= \alpha\) \(\textrm{ radians}\).
l'arc de cercle \(\substack{{\curvearrowright}\\{AM}}\) mesure \(s = \alpha R\)
(pour un radian, l'arc mesure \(s = R\))
l'aire du secteur circulaire \(AOM\) mesure \((1/2) ~\alpha ~R^{2}\)
Relations entre les trois unités d'un angle \(\alpha\)
mesure en radians \((\alpha_{r})\), degrés \((\alpha_{d})\), et grades \((\alpha_{g})\)
\(\frac{\alpha_{r}}{\pi} = \frac{\alpha_{d}}{180} = \frac{\alpha_{g}}{200}\)
Angle orienté
\(\widehat{AOM}\) est l'ange géométrique qui a une mesure :
\(\widehat{AOM} = \alpha\)
\(\left(\overrightarrow{OA}, \overrightarrow{OM}\right)\) est l'angle de vecteurs qui a une infinité de mesures :
\(\left(\overrightarrow{OA}, \overrightarrow{OM}\right) = \alpha + 2 k \pi \quad (k \in \mathbb{Z})\)
Parmi ces mesures, la "détermination principale" est la mesure qui appartient à \(] -\pi, +\pi ]\)
Le cercle trigonométrique
Dans un repère orthonormé \(\left(O,\vec{i}, \vec{j}\right)\).
Le cercle trigonométrique est le cercle de centre \(O\) et de rayon \(1\).
Par convention le sens de parcours positif est celui du sens inverse des aiguilles d'une montre.
Les lignes trigonométriques
Définition :
Le sinus, le cosinus, la tangente et la cotangente d'un arc constituent les lignes trigonométriques (ou fonctions circulaires) de l'arc.
On appelle sécante et cosécante d'un arc, respectivement l'inverse du cosinus et l'inverse du sinus et on écrit :
\(\textrm{s\'ec }\alpha = 1/\cos \alpha \textrm{ et } \textrm{cos\'ec }\alpha = 1/ \sin \alpha\)
Relations fondamentales
Sachant que :
\(\sin \alpha = \overline{OQ}\)
\(\cos \alpha = \overline{OP}\)
\(\tan \alpha = \overline{AT}\)
\(\textrm{cotan }\alpha = \overline{BS}\)
nous déterminons les relations suivantes :
Dans le triangle rectangle \(OPM\), on a :
\(\overline{OM}^{2} = \overline{OP}^{2} +\overline{PM}^{2} = \overline{OP}^{2} + \overline{OQ}^{2}\)
\(\cos^{2} \alpha + \sin^{2} \alpha = 1 ~(\forall \alpha \in \mathbb{R})\) (1)
Dans les triangles homothétiques \(OAT\) et \(OPM\), on a :
\(\frac{\overline{AT}}{\overline{PM}} = \frac{\overline{OA}}{\overline{OP}} \Leftrightarrow \overline{AT} = \overline{OA}\frac{\overline{PM}}{\overline{OP}}\)
\(\tan \alpha = \frac{\sin \alpha}{\cos \alpha} \left(\forall \alpha \in \mathbb{R} - \left(\frac{\pi}{2} + k \pi\right) k \in \mathbb{Z} \right)\) (2)
Dans les triangles homothétiques \(OBS\) et \(OQM\), on a :
\(\frac{\overline{BS}}{\overline{QM}} = \frac{\overline{OB}}{\overline{OQ}} \Leftrightarrow \overline{BS} = \overline{OB}\frac{\overline{OM}}{\overline{OQ}}\)
\(\textrm{cotan }\alpha = \frac{\cos \alpha}{\sin \alpha} = \frac{1}{\tan \alpha} (\forall \alpha \in \mathbb{R} - \{k \pi\} ~k \in \mathbb{Z})\) (3)
En divisant (1) par \(\cos^{2}\alpha\) nous obtenons : \(1 + \tan^{2} \alpha = \frac{1}{\cos^{2} \alpha}\)
\(\cos^{2} \alpha = \frac{1}{1 + \tan^{2} \alpha} \textrm{ et }\sin^{2} \alpha = \frac{\tan^{2} \alpha}{1 + \tan^{2} \alpha}\)