Trigonométrie hyperbolique
Définitions
On appelle sinus hyperbolique, l'application notée :
\(\begin{array}{ll}\textrm{sh }:&\mathbb{R} \mapsto \mathbb{R}\\& x \mapsto \textrm{sh}x = \frac{e^{x} - e^{-x}}{2} \end{array}\)
On appelle cosinus hyperbolique, l'application notée :
\(\begin{array}{ll}\textrm{ch }:&\mathbb{R} \mapsto \mathbb{R}\\& x \mapsto \textrm{ch}x = \frac{e^{x} + e^{-x}}{2} \end{array}\)
On appelle tangente hyperbolique, l'application notée :
\(\begin{array}{ll}\textrm{th }:&\mathbb{R} \mapsto \mathbb{R}\\& x \mapsto \textrm{th}x = \frac{\textrm{sh}x}{\textrm{ch}x}=\frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} = \frac{e^{2x}-1}{e^{2x} + 1}\end{array}\)
On appelle cotangente hyperbolique, l'application notée :
\(\begin{array}{ll}\textrm{coth }:&\mathbb{R}^{\ast} \mapsto \mathbb{R}\\& x \mapsto \textrm{coth}x = \frac{\textrm{ch}x}{\textrm{sh}x}=\frac{e^{x} + e^{-x}}{e^{x} - e^{-x}} = \frac{e^{2x}+1}{e^{2x} - 1}\end{array}\)
Remarque :
D'après les définitions de \(\textrm{sh } x\) et \(\textrm{ch }x\) nous avons :
\(\forall x \in \mathbb{R} \quad\textrm{ ch }x ≥ 1 \textrm{ et }\textrm{ch }x > \textrm{sh }x\)
Relations fondamentales
D'après la définition des applications \(\textrm{sh }\) et \(\textrm{ch }\) nous en déduisons :
\(\begin{array}{ll} \textrm{ch}x + \textrm{sh}x = e^{x} \\ \textrm{ch}x - \textrm{sh}x = e^{-x}\end{array}\forall x \in \mathbb{R}\)
En multipliant membre à membre ces deux relations :
\(\textrm{ch}^{2}x - \textrm{sh}^{2}x = 1\)
et en divisant par \(\textrm{ch}^{2} x\) :
\(1-\textrm{th}^{2}x = \frac{1}{\textrm{ch}^{2}x}\)
d'où :
\(\textrm{ch}^{2}x = \frac{1}{1-\textrm{th}^{2}x} \quad\textrm{ et }\quad\textrm{sh}^{2}x = \frac{\textrm{th}^{2}x}{1-\textrm{th}^{2}x}\)
Analogie entre applications circulaires et hyperboliques
D'après les formules d'Euler
\(\sin x = \frac{e^{jx} - e^{-jx}}{2j} \qquad \cos x = \frac{e^{jx} + e^{-jx}}{2}\)
\(\forall x \in \mathbb{R} \textrm{ avec } j^{2} = -1\)
les définitions des applications hyperboliques montrent la comparaison formelle suivante :
\(\textrm{sh }(jx) = j \sin x\) \(\textrm{ch }(jx) = \cos x\) \(\textrm{th }(jx) = j \tan x\) \(\textrm{coth }(jx) = - j \textrm{cotan x}\) | \(\sin (jx) = j \textrm{ sh }x\) \(\cos (jx) = \textrm{ ch }x\) \(\tan (jx) = j \textrm{ th }x\) \(\textrm{cotan }(jx) = - j \textrm{ coth }x\) |
La formule de Moivre
\((\cos x + j \sin x)^{n} = \left(e^{jx}\right)^{n} = e^{j n x} = \cos(nx) + j \sin(nx)\)
trouve une formule analogue en trigonométrie hyperbolique
\((\textrm{ch }x +\textrm{sh }x)^{n} = \left(e^{x}\right)^{n} = e^{n x} = \textrm{ch}(nx) + \textrm{sh}(nx)\)
De même la relation \(\cos^{2} x + \sin^{2} x = 1 ~\forall x \in \mathbb{R}\) conduit formellement à :
\(\cos^{2} (j x) + \sin^{2} (jx) = 1 \Leftrightarrow \textrm{ch}^{2} x + j^{2} \textrm{sh}^{2}x = \textrm{ch}^{2}x - \textrm{sh}^{2}x = 1\)
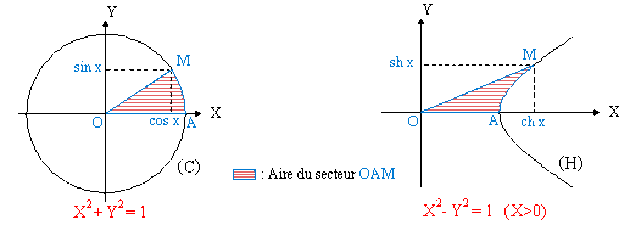
Dans le plan euclidien \(OXY\), si on considère :
d'une part le cercle centré à l'origine de rayon unité et d'équation : \(X^{2} + Y^{2} = 1\)
d'autre part la branche d'hyperbole équilatère, pour \(X > 0\) et d'équation : \(X^{2} - Y^{2} = 1\)
en désignant par x la moitié de l'aire du secteur \(OAM\), alors les coordonnées du point \(M\) sont :
\(M\) \((\cos x, \sin x)\) pour le cercle \((C)\) \(\Leftrightarrow \cos^{2}x + \sin^{2} x = 1\)
\(M\) \((\textrm{ch }x, \textrm{sh }x)\) pour l'hyperbole \((H)\) \(\Leftrightarrow \textrm{ch}^{2} x - \textrm{sh}^{2} x = 1\)