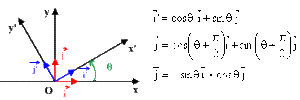Changement de base
On considère les deux bases \(B = (e_{1}, e_{2}, ..., e_{n})\) et \(B' = (e'_{1}, e'_{2}, ..., e'_{n})\) d'un même espace vectoriel \(\mathcal{E}\) de dimension \(n\).
Matrice de changement de base de B à B'
Les vecteurs de base de \(B'\) peuvent s'exprimer dans \(B\) selon les relations :
\(\left\{ \begin{array}{l} e'_{1} = a_{11}e_{1} + a_{21}e_{2} + \ldots + a_{n1}e_{n} \\ e'_{2} = a_{12}e_{1} + a_{22}e_{2} + \ldots + a_{n2}e_{n} \\ \ldots \\ e'_{n} = a_{1n}e_{1} + a_{2n}e_{2} + \ldots + a_{nn}e_{n} \end{array}\right.\)
On appelle matrice de passage de \(B\) à \(B'\) la matrice carrée \(P\) définie par :
\(P = \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & \ldots \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & \ldots & \ldots & a_{nn} \end{pmatrix}\)
Les colonnes d'indice \(i\) sont formées par les composantes \(e'_{i}\) dans la base \(B\).
La matrice \(P^{-1}\) sera donc la matrice de passage de \(B'\) à \(B\).
(voir exemple ci-dessous : Matrice de passage)
Si \(B\) et \(B'\) sont deux bases orthonormées de \(\mathcal{E}\), la matrice de passage \(P\) est dite orthogonale et vérifie : \(P^{-1} =~^{t}~P\).
(voir exemple ci-dessous : Matrice de passage orthogonale)
Exemple : Matrice de passage
Soit \(B = (e_{1},e_{2},e_{3})\) la base canonique de \(\mathbb{R}_{3}\).
Sachant que les vecteurs de la base \(B'\) sont définis par : \(\left\{ \begin{array}{l} e'_{1} = e_{1} - e_{2} + e_{3} \\ e'_{2} = e_{1} + e_{2} - e_{3} \\ e'_{3} = e_{1} - e_{3} \end{array} \right.\),
la matrice de passage \(P\) de \(B\) à \(B'\) est la matrice carrée : \(\color{red} P = \begin{pmatrix} 1 & 1 & 1 \\ -1 & 1 & 0 \\ 1 & - 1 & - 1 \end{pmatrix}\)
La matrice \(P^{-1}\) sera la matrice de passage de \(B'\) à \(B\), obtenue en explicitant les vecteurs de base de \(B\) dans \(B'\).
\(\left\{ \begin{array}{l} e'_{1} = e_{1} - e_{2} + e_{3} \\ e'_{2} = e_{1} + e_{2} - e_{3} \\ e'_{3} = e_{1} - e_{3} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} e_{1} = \frac{e'_{1}}{2} - \frac{e'_{2}}{2}\\ \\ e_{2} = e'_{2} - e'_{3} \\ \\ e_{3} = \frac{e'_{1}}{2} + \frac{e'_{2}}{2} - e'_{3} \end{array} \right.\)
\(\color{red} P^{-1} = \begin{pmatrix} 1/2 & 0 & 1/2 \\ 1/2 & 1 & 1/2 \\0 & -1 & -1 \end{pmatrix}\)
Exemple : Matrice de passage orthogonale
Matrice de rotation dans le plan autour de \(O\).
Soient \(B(\overset{\rightarrow}{i}, \overset{\rightarrow}{j})\) et \(B' (\overset{\rightarrow}{i}', \overset{\rightarrow}{j}')\) deux bases orthonormées.
Pour une rotation autour de \(O\) d'un angle \(q\), nous avons:
La matrice de passage \(P\) de \(B\) à \(B'\) est donc : \(\color{red} P = \begin{pmatrix} \cos{\theta}& -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix}\)
La matrice \(P^{-1}\) s'obtient en explicitant \(\overset{\rightarrow}{i}\) et \(\overset{\rightarrow}{j}\) en fonction de \(\overset{\rightarrow}{i'}\) et \(\overset{\rightarrow}{j'}\) ou en changeant \(q\) en \(-q\) :
\(\color{red} P^{-1} = \begin{pmatrix} \cos{\theta}& +\sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix}\)
La matrice de passage de ces deux bases orthonormées vérifie bien la relation : \(\color{red} P^{-1} =~^{t}P\)
Conséquences d'un changement de base
Sur les composantes d'un vecteur
En posant \(X\) la matrice unicolonne des composantes dans \(B\) du vecteur \(x \in \mathcal{E}\),
\(x = x_{1}e_{1} + x_{2}e_{2} + \ldots + x_{n}e_{n}\),
et \(X'\) celle du même vecteur \(x\) dans \(B'\) :
\(x = x'_{1}e'_{1} + x'_{2}e'_{2} + \ldots + x'_{n}e'_{n}\),
nous aurons alors : \(\color{red} X = P X'\) ou \(\color{red} X' = P^{-1} X\), où \(P\) est la matrice de passage de \(B\) à \(B'\).
Démonstration :
Soit un vecteur \(x \in \mathcal{E}\) de composantes \((x_{1}, x_{2}, ..., x_{n})\) dans la base \(B\) \((e_{1}, e_{2}, ..., e_{n})\) et \((x'_{1}, x'_{2}, ..., x'_{n})\) dans \(B'\) \((e'_{1}, e'_{2}, ..., e'_{n})\).
Ce vecteur s'exprimera dans les deux bases sous la forme :
\(x = x_{1}e_{1} + x_{2}e_{2} + ... + x_{n}e_{n}\) dans \(B\)
\(x = x'_{1}e'_{1} + x'_{2}e'_{2} + ... + x'_{n}e'_{n}\) dans \(B'\)
Les vecteurs de \(B'\) étant reliés aux vecteurs de \(B\) par la matrice de passage :
Nous aurons donc :
\(x = x'_{1}(a_{11}e_{1} + a_{21}e_{2} + \ldots + a_{n1}e_{n}) + x'2(a_{12}e_{1} + a_{22}e_{2} + \ldots + a_{n}2x_{n}) + \ldots \\ + x'_{n}(a_{1n}e_{1} + a_{2n}e_{2} + \ldots + a_{nn}e_{n})\)
\(x = (a_{11} x'_{1} + a_{12} x'_{2} + \ldots + a_{1n} x'_{n}) e_{1} + (a_{21} x'_{1} + a_{22} x'_{2} + \ldots + a_{2n} x'_{n}) e_{2} + \ldots \\ +(a_{n1} x'_{1} + a_{n2} x'_{2} + \ldots + a_{nn} x'_{n}) e_{n}\)
Par identification des composantes :
\(\left\{ \begin{array}{r c l} x_{1} & = & a_{11}x'_{1} + a_{12}x'_{2} + \ldots + a_{1n}x'_{n} \\ x_{2} & = & a_{21}x'_{1} + a_{22}x'_{2} + \ldots + a_{2n}x'_{n} \\ \ldots & & \\ x_{n} & = & a_{n1}x'_{1} + a_{n2}x'_{2} + \ldots + a_{nn}x'_{n} \end{array} \right.\)
soit sous forme matricielle :
\(\begin{pmatrix} x_{1} \\ x_{2} \\ \ldots \\ x_{n} \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & \ldots \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & \ldots & \ldots & a_{nn} \end{pmatrix} \begin{pmatrix} x'_{1} \\ x'_{2} \\ \ldots \\ x'_{n} \end{pmatrix}\Leftrightarrow \color{red} X = PX'\)
Exemple : Transformation des composantes d'un vecteur
Soient \(B(\overset{\rightarrow}{i}, \overset{\rightarrow}{j})\) et \(B' (\overset{\rightarrow}{i}', \overset{\rightarrow}{j}')\) deux bases orthonormées directes cartésienne et polaire.
Exprimons les vecteurs de base de \(B'\) dans \(B\).
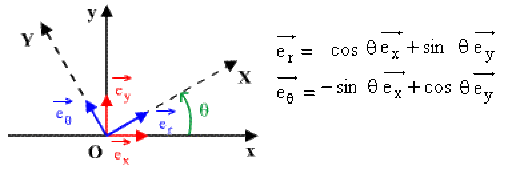
La matrice de passage \(P\) de \(B\) à \(B'\) est définie par :
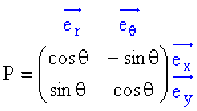
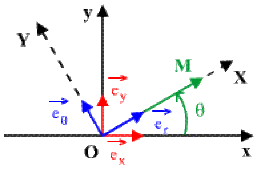
Un point \(M\) du plan peut être repéré soit par ses coordonnées cartésiennes \((x,y)\), soit par ses coordonnées polaires \((r,q)\).
Explicitons le vecteur position \(\overset{\rightarrow}{\textrm{OM}} = x \overset{\rightarrow}{e_{x}} + y \overset{\rightarrow}{e_{y}}\) dans la base polaire \(B'\).
Posons \(\overset{\rightarrow}{\textrm{OM}} = x'\overset{\rightarrow}{e_{r}} + y' \overset{\rightarrow}{e_{\theta}}\) dans \(B'\), d'où :
\(\begin{pmatrix} x' \\ y' \end{pmatrix} = P^{-1} \begin{pmatrix} x \\ y \end{pmatrix} \Leftrightarrow \begin{pmatrix} x' \\ y'\end{pmatrix} = \begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\)
\(\color{red}x' = x \cos{\theta} + y \sin{\theta}\)
\(\color{red}y' = -x \sin{\theta} + y \cos{\theta}\)
D'après les relations entre les composantes cartésiennes et polaires :
Sur la matrice d'une application linéaire
Soit
\(f\) une application linéaire de \(\mathcal{E}\) dans \(\mathcal{E}\) (endomorphisme),
\(A\) (resp. \(A'\)) une matrice carrée d'ordre \(n\) associée à \(f\) dans la base \(B\) (resp. \(B'\)),
\(P\) la matrice de passage de \(B\) à \(B'\),
\(X\) (resp. \(X'\)) et \(Y\) (resp. \(Y'\)) les matrices colonnes des composantes des vecteurs \(x\) et \(y\) dans \(B\) (resp. \(B'\))
alors, si \(y = f(x) \Leftrightarrow \left\{ \begin{array}{l} \textrm{dans}~B : Y = AX \\ \textrm{dans}~B' : Y' = AX' \end{array} \right.\)
Comme \(X = PX'\) et \(Y = PY'\), alors :
\(Y = PY' = AX = APX'\) soit en prémultipliant par \(P^{-1}\) : \(P^{-1}PY' = P^{-1}APX' \Rightarrow Y' = P^{-1}APX' \Rightarrow \color{red} A' = P^{-1}AP\)
Exemple : Transformation de la matrice d'une application linéaire
Soit \(\mathcal{E}\) un espace vectoriel sur \(\mathbb{R}\), de dimension \(3\), et soit \(f\) l'endomorphisme de \(\mathcal{E}\) ayant pour matrice dans la base \(B = (e_{1}, e_{2}, e_{3})\) de \(\mathcal{E}\).
\(A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -2 & -1 \\ 0 & 0 & 1 \end{pmatrix}\)
On pose : \(e'_{1} = e_{1}~;~e'_{2} = e_{2}~;~e'_{3} = -(1/3) e_{2} + e_{3}\).
Calculer la matrice \(A'\) de \(f\) relativement à la base \(B' = (e'_{1}, e'_{2}, e'_{3})\).
Par définition : \(A' = P^{-1}AP\) avec \(P\) la matrice de passage de \(B\) dans \(B'\) :
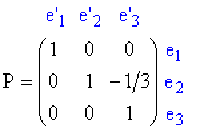
La matrice inverse \(P^{-1}\) peut s'obtenir en explicitant les vecteurs de base de \(B\) en fonction des vecteurs de base de \(B'\) :
\(\begin{array}{r c l}e'_{1} = e_{1} & & e_{1} = e'_{1} \\& \Leftrightarrow & \\e'_{2} = e_{2} & & e_{2} = e'_{2} \\e'_{3} = -\frac{1}{3} e_{2} + e_{3} & & e_{3} = \frac{1}{3}e'_{2} + e'_{3}\end{array}\)
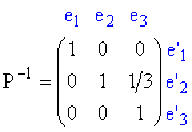
d'où \(A' = P^{-1} AP = \begin{pmatrix} 1 & 0& 0 \\ 0 & 1 & 1/3 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0& 0 \\ 0 & -2 & -1 \\ 0 & 0 & 1\end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & -1/3 \\ 0 & 0 & 1 \end{pmatrix}\)
\(\color{red} A' = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & 1\end{pmatrix}\)
On remarque que ce changement de base a pour effet de donner une forme plus simple à la matrice de \(f\) : on a diagonalisé la matrice de \(f\).