Puissance instantanée

Soit un dipôle[1] parcouru par un courant sinusoïdal[2] d'intensité[3] :

\(i(t) = I_m \cos\omega t\)

et aux bornes[4] duquel on observe une tension :

\(u(t) = U_m \cos (\omega t + \varphi)\)

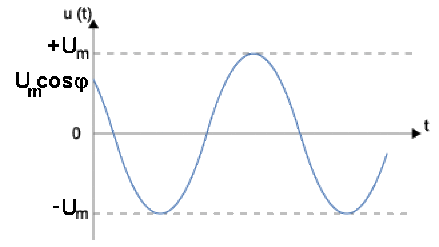
par analogie avec les lois du courant continu, on appelle puissance instantanée :

\(p(t) = u(t).i(t) = U_m I_m \cos ( \omega t+\varphi).\cos \omega t\)

en appliquant la relation :

\(\cos a.\cos b = (1/2)[\cos ( a+b) + \cos ( a-b) ]\)

on obtient :

\(p(t) = (1/2)U_m.I_m[\cos(2\omega t + \varphi) + \cos \varphi]\)

dont la courbe est représentée ci-dessous :

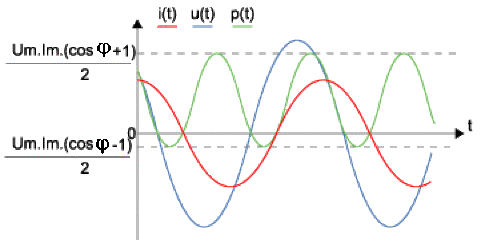
On voit que la puissance instantanée oscille, à une fréquence[5] double de celle du courant, entre

\(\frac{1}{2}[U_m.I_m(\cos\varphi+1)]\textrm{ et }\frac{1}{2}[U_m.I_m(\cos\varphi-1)]\)

sauf dans le cas particulier où \(\varphi = 0\) , la valeur minimal de la puissance est donc négative pour les dipôles étudiés \(\big(-\frac{\pi}{2}\leq\varphi\leq\frac{\pi}{2}\big)\)