Puissance moyenne, facteur de puissance
Définition :
Par définition, la valeur moyenne d'une fonction périodique est définie par :
\(\big\langle f(t)\big\rangle=\frac{1}{T}\displaystyle{\int_0^Tf(t).dt}\)
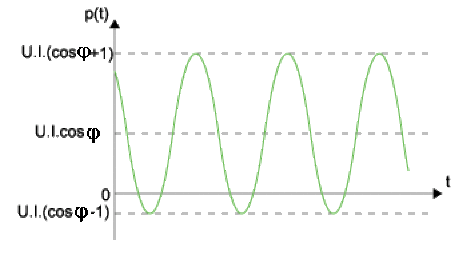
La moyenne sur une période de \(\cos(2\omega t + \varphi)\) étant nulle, il vient :
\(P=\big\langle p(t)\big\rangle=\frac{1}{2}U_m.I_m.\cos\varphi\)
soit, en utilisant les valeurs efficaces[1] : \(U=\frac{U_m}{\sqrt{2}} ;\;I=\frac{I_m}{\sqrt{2}}\)
\(P=U.I.\cos\varphi\)
Remarque :
Comme : \(U = Z.I \textrm{ et } R = Z\cos \varphi,\textrm{ on a } P = R.I^2\) , expression identique à celle obtenue en courant continu. Donc, dans un dipôle passif[3] toute la puissance consommée est dissipée par effet Joule[4]. On peut aussi exprimer P en fonction de la tension : puisque \(I = U/Z\), on a \(P = R(U^2/Z^2)\) ; dans ce cas , l'expression diffère de celle obtenue en courant continu.