Circuit d'allumage
Durée : 10 mn
Note maximale : 11
Question
Le circuit d'allumage d'un moteur à explosion peut être modélisé par le montage suivant :
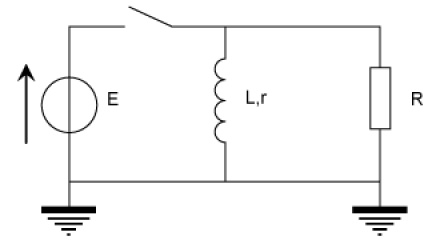
\(E = 12 \mathrm{ V}\) (batterie).
La bobine (bobine d'allumage) est résistive et peut être schématisée par une résistance \(r = 8 \mathrm{ } \Omega\) en série avec une inductance \(L = \mathrm{0,8 H}\).
Le circuit d'allumage est assimilé à une résistance \(R = 1 \mathrm{ k} \Omega\).
On notera \(i_B\) le courant dans la bobine et \(i_R\) celui dans \(R\).
L'interrupteur est fermé, et le régime permanent établi :
Exprimer la tension \(u_B\) aux bornes de la bobine en fonction de \(i_B\). Que devient cette expression en régime permanent continu ?
Calculer \(i_B\) et \(i_R\) en régime permanent continu.
A l'instant \(t = 0\), on ouvre l'interrupteur. On pose \(i = i_B\).
Etablir l'équation différentielle vérifiée par \(i(t)\) et la résoudre. La condition initiale sera obtenue en considérant la continuité de \(i_B\).
En déduire \(u_R(t)\) et sa valeur à \(t = 0^{+}\). Quel est l'intérêt de ce montage ?
Solution
Quand l'interrupteur est fermé, la tension est la même aux bornes des 3 branches : \(E = u_B = u_R\) ;
\(\displaystyle{ u_B = L . \frac{\mathrm{d} i_B}{\mathrm{d} t} + r . i_B(t) }\) ;
\(u_R = R . i_R(t)\) (3 pts)
Quand le régime permanent est atteint :
\(\displaystyle{ \frac{\mathrm{d} i_B}{\mathrm{d} t} =0 }\), et \(\displaystyle{ i_B = \frac{E}{r} = \frac{12}{8} = \mathrm{1,5 A} }\) ;
dès la fermeture de l'interrupteur, \(\displaystyle{ i_R = \frac{E}{R} = \frac{12}{10^3} = 12 \mathrm{ mA} }\) (2 pts)
Quand l'interrupteur est ouvert, il n'y a plus qu'une seule maille dans laquelle passe un courant unique d'intensité \(i(t)\) ; l'application de la loi des mailles donne :
\(\displaystyle{ L . \frac{\mathrm{d} i}{\mathrm{d} t} + r . i(t) + R . i(t) = 0 }\)
qui peut s'écrire : \(\displaystyle{ \big[\frac{L}{r + R}\big] . \frac{\mathrm{d} i}{\mathrm{d} t} + i(t) = 0 }\)
Il s'agit de l'équation d'un circuit du premier ordre dont la constante de temps est \(\displaystyle{ \tau = \frac{L}{r + R} }\). (2 pts)
La solution de cette équation est \(\displaystyle{ i(t) = K . \mathrm{e}^{-{t}/{\tau}} }\), où \(K\) est une constante donnée par les conditions initiales.
L'intensité dans une bobine ne peut varier que de façon continue, selon la loi de Lenz ; donc :
\(\displaystyle{ i(0) = i_B = \frac{E}{r} = K }\)
finalement : \(\displaystyle{ i(t) = \frac{E}{r} . \mathrm{e}^{-{t}/{\tau}} }\)
L'intensité à travers le circuit d'allumage décroît progressivement à partir de \(\displaystyle{ \frac{E}{r} = 12 \mathrm{ mA}}\). (2 pts)
D'après la loi d'Ohm, \(\displaystyle{ u_R = R . i(t) = E . \frac{R}{r} }\) pour \(t = 0\) .
Application numérique :
\(\displaystyle{ u_R = \frac{12 . 10^3}{8} = \mathrm{1,5} . 10^3 \mathrm{ V}}\)
\(\Rightarrow\) le montage permet d'avoir une tension d'allumage importante (\(1500 \mathrm{ V}\)) à partir d'une batterie délivrant \(12 \mathrm{ V}\). (2 pts)