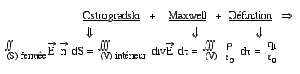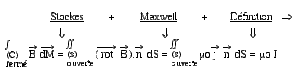a. Equations de Maxwell et application
Rappel :
Les équations de Maxwell fournissent des relations entre les variations des grandeurs électromagnétiques (\(\vec E\), \(\vec B\), \(\vec D\), \(\vec H\)) en tout point \(M(x, y, z)\) de l'espace.
Les variations en fonction du temps s'expriment par la dérivée partielle par rapport au temps, les variations en fonction des coordonnées d'espace s'expriment par l'intermédiaire des opérateurs différentiels : rotationnel et divergence.
Ces relations sont locales : elles relient les variations au point \(M (x, y, z)\) des grandeurs électromagnétiques à chaque instant.
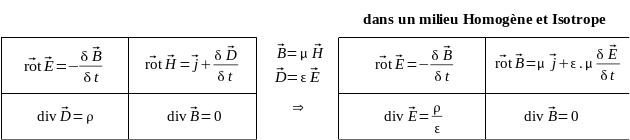
Dans ce qui suit, on ne traite pas le cas général des milieux matériels réels, mais simplement le cas des milieux homogènes et isotropes : dans ce cas, l'excitation magnétique \(\vec B\) est un vecteur proportionnel à l'induction magnétique \(\vec H\), et l'induction électrique \(\vec D\) est proportionnelle au champ électrique \(\vec E\).
Notations (valeurs en unités MKSA) :
\(\vec B\) induction magnétique
\(\vec H\) excitation magnétique
\(\vec D\) induction électrique
\(\vec E\) excitation électrique
\(\mu\) perméabilité magnétique du milieu
\(\mu_0\) perméabilité magnétique du vide : \(\mu_0 = 4.\pi.10^{-7}\)
\(\mu_r\) perméabilité magnétique relative : \(\mu = \mu_0 = \mu_r\)
\(\varepsilon\) permittivité électrique
\(\varepsilon_r\) permittivité électrique relative : \(\varepsilon = \varepsilon_0 . \varepsilon_r\)
\(\varepsilon_0\) permittivité électrique du vide avec : \(\displaystyle{\frac{1}{4 . \pi . \varepsilon_0} = 9 . 10^9}\)
\(\mathrm{c}\) vitesse de l'onde électromagnétique dans le vide \(\mathrm{c}^2 = \frac{1}{\varepsilon_0 . \mu_0} = 9 . 10^{16} ~ \mathrm{m/s}\)
Opérateurs différentiels et théorèmes
Rappel : Opérateurs différentiels
En utilisant l'opérateur symbolique NABLA : \(\vec \nabla\) : \(\Big( \frac{\partial}{\partial x} ~ , ~ \frac{\partial}{\partial y} ~ , ~ \frac{\partial}{\partial z} \Big)\)
\(\overrightarrow{\mathrm{grad}} (f) = \vec \nabla f\)
\(\overrightarrow{\mathrm{rot}} ~ ({\vec V}) = \vec \nabla \wedge \vec V\)
\(\mathrm{div} ~ ({\vec V}) = \vec V \wedge \vec V\)
\(\Delta f = \vec \nabla . \vec \nabla f\)
Théorème :
Sous réserve des conditions de dérivabilité, on a, pour toute fonction \(f\) des variables \((x,y,z)\) et pour toute fonction vectorielle \(\vec V\) des variables \((x,y,z)\) :
\((1) ~~ \overrightarrow{\mathrm{rot}} (\overrightarrow{\mathrm{grad}} ~ f) = 0\)
\((2) ~~ \mathrm{div} (\overrightarrow{\mathrm{grad}} ~ f) = \Delta f\)
\((3) ~~ \mathrm{div} [\overrightarrow{\mathrm{rot}} ~ (\vec V)] = 0\)
\((4) ~~ \Delta \vec V = \overrightarrow{\mathrm{grad}} [\mathrm{div} ~ (\vec V)] - \overrightarrow{\mathrm{rot}} [\overrightarrow{\mathrm{rot}} ~ (\vec V)]\)
Equations de Maxwell
Ces équations sont LOCALES , i.e. ce sont des relations (en tout point \(M\)), entre les valeurs en \(M\) de ces fonctions
Exemple : en un point \(M\) tel que :
la densité de courant est nulle : \(\vec j (M) = 0\)
et la densité de charge est nulle : \(\rho(M) = 0\)
\(\Rightarrow\) en ce point
\(\begin{array}{cc} \overrightarrow{\mathrm{rot}} \vec H = \frac{\partial \vec D}{\partial t} \\ \mathrm{div} \vec D = 0 \end{array}\)
Conséquences
Cas particuliers : ELECTROSTATIQUE et MAGNETOSTATIQUE : \frac{\partial}{\partial t} = 0
ELECTROSTATIQUE : équation de POISSON
Champ Electrique \(\vec E\) dérivant d'un potentiel scalaire \(\varphi\) :
\(\vec E = - \overrightarrow{\mathrm{grad}} (\varphi)\)
\(\textrm{[avec Th\'eo.(1)]} \Leftrightarrow \overrightarrow{\mathrm{rot}} (\vec E) = \vec 0\)
(par définition)
Champ magnétique \(\vec B\) dérivant d'un potentiel vecteur \(\vec A\) :
\(\vec B = \overrightarrow{\mathrm{rot}} (\vec A)\)
\(\textrm{[avec Th\'eo.(3)]} \Leftrightarrow \mathrm{div} (\vec B) = 0\)
\(\Leftrightarrow \frac{\partial}{\partial t} \vec B = 0 \Leftrightarrow \mathrm{Electrostatique}\)
ELECTROSTATIQUE
\(\displaystyle{\Leftrightarrow \vec E = - \overrightarrow{\mathrm{grad}} (\varphi) ~~ \mathrm{et} ~~ \mathrm{div} ~ \vec E = \frac{\rho}{\varepsilon}}\)
avec Théo.(2)
\(\Rightarrow\)
Equation de POISSON :
\(\displaystyle{\Delta \varphi(M) + \frac{\rho(M)}{\varepsilon(M)} = 0}\)
Théorème de Gauss et Théorème d'Ampère
Equations de propagation
En dehors des charges et des courants, les équations de Maxwell donnent :
\(\vec E = 0\)
\(\displaystyle{\overrightarrow{\mathrm{rot}} ~ \vec B = \varepsilon . \mu \frac{\partial \vec E}{\partial t}}\)
Avec le Théorème (4), le calcul des Laplaciens \(\Delta \vec E\) et \(\Delta \vec B\) donne :
\(\displaystyle{\Delta \vec E = \varepsilon . \mu \frac{\partial^2 \vec E}{\partial t^2}}\)
\(\displaystyle{\Delta \vec B = \varepsilon . \mu \frac{\partial^2 \vec B}{\partial t^2}}\)
Chacune de ces équations se résout en projection : les équations projetées admettent (pour les composantes) de \(\vec E\) et de \(\vec B\) des solutions de la forme :
sur Ox :
\(f(\vec u_x . \vec r \pm Vt)\)
sur Oy :
\(g(\vec u_y . \vec r \pm Vt)\)
sur Oz :
\(h(\vec u_z . \vec r \pm Vt)\)
Remarque : A propos des solutions :
Dans un milieu homogène et isotrope : il n'y a propagation du champ (\(\vec E\), \(\vec B\)) que si : \(\vec u_x = \vec u_y = \vec u_z = \vec u\) .
Dans le cas général d'une propagation quelconque : le vecteur \(\vec u\) (direction de propagation) dépend de \(M\), soit \(\vec u(M)\).
Dans le cas particulier où le vecteur \(\vec u\) est constant \(\Rightarrow\) la direction de propagation est fixe.
Onde Plane
Définition : Onde plane et plan d'onde
Une onde est dite plane si, à tout instant, l'état de cette onde est invariant dans tout plan orthogonal à une direction fixe, définie par un vecteur constant \(\vec u\).
Tout plan orthogonal à ce vecteur \(\vec u\) est appelé plan d'onde.
En particulier : une onde qui se propage selon la direction définie par un vecteur unitaire \(\vec u\) constant est, à tout instant, invariante dans tout plan orthogonal à ce vecteur \(\vec u\).