d. Signification physique
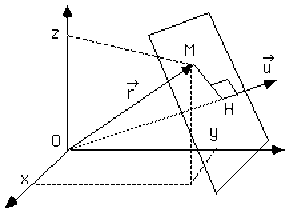
Le point \(M\) est défini par le vecteur \(\vec r\) de composantes \((x, y, z)\). Le produit scalaire \(\vec u . \vec r\) représente la distance \(OH\) mesurée le long de la direction \(\vec u\) :
depuis l'origine \(O\)
jusqu'au point \(H\) situé dans le même plan orthogonal à \(\vec u\) que le point \(M\).
On notera : \(OH = a\).
L'argument \(\phi\) peut alors s'exprimer : \(\phi = \vec u . \vec r ± V.t = a ± V.t\)
L'argument \(\phi\) reprend donc la même valeur après une distance \(\partial a\) et un temps \(\partial t\) tels que :
\(a ± V.t = (a + \partial a) ± V. (t + \partial t)\) soit, en simplifiant : \(\partial a ± V. \partial t = 0\).
Les solutions possibles sont : \(\begin{array}{l} \phi = \alpha - \varsigma . \tau ~,~ \alpha \omega \varepsilon \chi V = + \frac{\partial a}{\partial t} \\ f = a + V. t , \mathrm{ avec } V = - \frac{\partial a}{\partial t} \end{array}\)
Cette relation restant vraie lorsque \(\partial a\) tend vers \(0\), le coefficient \(V\) est donc la vitesse de la propagation :
dans le sens de \(\vec u\) (ou sens progressif) si \(\phi = \vec u . \vec r - V.t\)
dans le sens opposé de \(\vec u\) (ou sens régressif) si \(\phi = \vec u . \vec r + V.t\)
La solution de l'équation projetée, qui est de la forme : \(E_x (\phi) = E_x (a ± V.t)\), reprend donc aussi la même valeur après une distance \(\partial a\) et un temps \(\partial t\), tels que \(\partial a\) représente la translation de la composante \(E_x\) pendant le temps \(\partial t\).
La solution \(E_x (\phi) = E_x (a ± V.t)\) représente la translation de la composante \(E_x\) de \(\vec E\)
dans la direction du vecteur unitaire \(\vec u\)
avec la vitesse de propagation \(V\)
dans le sens progressif (sens de \(\vec u\)) si \(\phi = a - V.t\)
ou dans le sens régressif (sens opposé de \(\vec u\)) si \(\phi = a + V.t\)
On voit que l'équation de propagation n'exige pas que les composantes de \(\vec E\) et de \(\vec B\) se propagent dans la même direction \(\vec u\) et le même sens.
Bien entendu il peut exister dans une certaine région de l'espace, plusieurs sources de vibrations électromagnétiques dont les ondes se superposent et se propagent dans différentes directions.
Cette propriété est une conséquence directe de la linéarité de l'équation de propagation : toute combinaison linéaire de 2 solutions est aussi solution de l'équation de propagation.
Cependant :
S'il s'agit de la propagation des composantes du champ \(( \vec E, \vec B )\) produit par une source, alors on ne retiendra comme solution que celles traduisant une propagation de chacune des 3 composantes du vecteur champ \(\vec E\) et du vecteur champ \(\vec B\) :
dans la direction du même vecteur unitaire \(\vec u\)
dans le même sens (que ce sens soit progressif ou régressif)
à la vitesse : \(V = \frac{1}{\sqrt{\varepsilon . \mu}}\) définie par les caractéristiques \(\varepsilon\) et \(\mu\) du milieu.