Réflexion sur un diélectrique en incidence normale
Partie
Question
-A- Coefficients de Réflexion et de Transmission d'un dioptre plan séparant l'air (indice 1) et un verre (d'indice n)
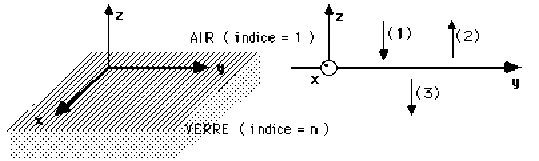
Une onde électromagnétique plane \((1)\) monochromatique de pulsation \(\omega_1\) dont le champ électrique est polarisé suivant \(Ox\) se propage dans l'air (à la vitesse : \(\textrm{c}\)) selon les \(z\) décroissants.
Ce champ sera représenté en notation complexe : \(\vec E_i = E_{io} . \vec i . \exp \big[ \textrm{j} . ( \omega . t - \vec K_1 . \vec r) \big]\) ,
\(K_1\) désignera la norme du vecteur d'onde \(\vec K_1\).
Donner l'expression de \(K_1\) puis de \(\vec K_1\) en fonction de \(\textrm{c}\) et de \(\omega\).
Rappeler la relation entre \(\vec E\) et \(\vec B\), parties variables d'une onde électromagnétique plane de vecteur d'onde \(\vec K\).
Mettre cette relation sous la forme : \(\vec B = \frac{1}{\omega} \vec K \wedge \vec E\)
Exprimer \(\vec E_1\) en fonction de \(z\) et de \(t\). En déduire le champ magnétique associé : \(\vec B_1\) dans l'onde \((1)\).
Cette onde \((1)\) arrivant sur le dioptre plan \((z = 0)\) se trouve : partiellement réfléchie [onde notée \((2)\)] et partiellement transmise [onde notée \((3)\)].
On admettra que les ondes \((2)\) et \((3)\) ont même direction de polarisation, même direction de propagation et même pulsation que l'onde incidente \((1)\), et sont respectivement déphasées de \(\theta_2\) et \(\theta_3\) par rapport à l'onde \((1)\).
Exprimer le vecteur d'onde \(\vec K_2\) de l'onde \((2)\).
Exprimer les champs \(\vec E_2\) et \(\vec B_2\) en fonction de l'amplitude \(E_{02}\) du champ électrique de l'onde \((2)\).
Exprimer le vecteur d'onde \(\vec K_3\) de l'onde \((3)\) en fonction de \(\textrm{c}\), \(\omega\) et \(n\) (indice du verre).
En déduire l'expression des champs \(\vec E_3\) et \(\vec B_3\) en fonction de l'amplitude \(E_{03}\) du champ électrique de l'onde \((3)\).
L'énergie d'une vibration électrique étant proportionnelle au carré de son amplitude, on définit pour une surface son pouvoir de :
Réflexion : \(R = \left[ \frac{E_{02}}{E_{01}} \right]^2 ~~~~\) et de Transmission : \(T = \left[ \frac{E_{03}}{E_{01}} \right]^2\)
Exprimer les composantes tangentielles et normales de \(\vec E\) et de \(\vec B\) relativement à la surface \(z = 0\).
Exprimer les relations de continuité pour \(\vec E\) et \(\vec H = \frac{\vec B}{\mu_0}\) .
En déduire 2 relations entre \(E_{01}\) , \(E_{02}\) et \(E_{03}\) , puis les expressions des pouvoirs de Réflexion \(R\) et de Transmission \(T\).
-B- Couche anti-reflet (d'indice \(n_1\)) sur un verre (d'indice \(n\))
Dans le dispositif optique représenté ci-dessous, on notera :

Le champ électrique \(\vec E_1\) de l'onde \((1)\) a les caractéristiques de celui étudié en -A-
Procéder comme en -A.2- pour expliciter complètement :
\(\vec E_1\) et \(\vec B_1\) en fonction de \(E_{01}\), \(\omega\), \(z\), \(t\) et \(\textrm{c}\).
\(\vec E_2\) et \(\vec B_2\) en fonction de \(E_{02}\), \(\omega\), \(z\), \(t\), \(n_1\) et \(\textrm{c}\).
\(\vec E_3\) et \(\vec B_3\) en fonction de \(E_{03}\), \(\omega\), \(z\), \(t\), \(n\) et \(\textrm{c}\).
\(\vec E_4\) et \(\vec B_4\) en fonction de \(E_{04}\), \(\omega\), \(z\), \(t\), \(n_1\) et \(\textrm{c}\).
\(\vec E_5\) et \(\vec B_5\) en fonction de \(E_{05}\), \(\omega\), \(z\), \(t\) et \(\textrm{c}\).
Ecrire les équations de continuité de \(\vec E\) et \(\vec H = \frac{\vec B}{\mu_0}\) aux surfaces : \(~ (S) [z = 0] ~\) et \(~ (S') [z = -e]\) .
En déduire 4 relations, reliant : \(E_{01}\), \(E_{02}\), \(E_{03}\), \(E_{04}\) et \(E_{05}\).
On pose : \(~~ E_2 = E_{02} . \exp \big[-\textrm{j} . \omega . n_1 . \frac{e}{\textrm{c}} \big] ~~\) et \(~~ E_4 = E_{04} . \exp \big[ -\textrm{j} . \omega . n_1 . \frac{e}{\textrm{c}} \big]\)
Considérant les relations de passage en \((S')\), montrer que l'on peut éliminer \(E_{03}\) et exprimer simplement \(E_4\) en fonction de \(E_2\).
Si la couche \((n_1)\) est une lame quart d'onde \(\left[ e = \frac{\lambda_1}{4} \right]\) montrer qu'alors : \(\omega . n_1 . \frac{e}{\textrm{c}} = \frac{\pi}{2}\)
Exprimer simplement \(E_{04}\) en fonction de \(E_{02}\).
Considérant les relations de passage en \((S)\), exprimer \(\frac{E_{05}}{E_{01}}\) .
Exprimer le pouvoir de Réflexion \(R\) du système considéré ici.
A quelle condition est-il minimum ? Cette condition peut-elle être remplie quelle que soit la longueur d'onde de la lumière incidente ?
Exprimer \(E_2\) en fonction de \(E_1\) pour une lame quart d'onde, pour une lame demi onde.
Aide simple
Revoir la structure d'une onde électromagnétique plane.
Revoir les conditions de réflexion sur un dioptre.
Superposition d'une onde progressive et d'une onde régressive d'amplitudes différentes.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Ici, la réflexion de l'onde n'est pas totale :le champ électrique réfléchi qui est représenté (qui se propage en sens inverse du champ électrique incident), a la même fréquence mais une amplitude plus petite que celle de l'incident.
La somme de ces deux champs électriques est pseudo-stationnaire.
Idem pour la somme des deux champ magnétiques
La réflexion de l'onde n'est pas totale : le champ électromagnétique est ici représenté par le champ électrique et le champ magnétique correspondants. Vérifier les relations de continuité sur le dioptre...
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Rappel de cours
Voir la page Résultat général
Solution détaillée
- A - Traversée par une surface plane.
- A.1 -
- A.1.1 -
Propagation dans le sens de \(- \vec k\) \(~~~~ \Rightarrow ~~\) \(\vec K_1 = - K_1 . \vec k\) .
Vitesse de propagation de l'onde électromagnétique dans l'air (\(\approx \textrm{dans le vide}\)) : \(~ \textrm{c} = \frac{\omega}{K_1} ~\) soit \(K_1 = \frac{\omega}{\textrm{c}}\) .
- A.1.2 -
Pour une onde plane \(( \vec E, \vec B )\) : \(\vec B = \frac{1}{v} \vec u \wedge \vec E\) où \(v\) est la vitesse de propagation et \(\vec u\) le vecteur unitaire dans le sens de la propagation.
\(\Rightarrow ~~ \vec u = \frac{\vec K}{K}\) \(~~~~ \Rightarrow ~~\) \(\vec B = \frac{1}{v} \frac{1}{K} \vec K \wedge \vec E ~~\)
et, comme \(v K = \omega\) : \(~~~~ \Rightarrow ~~ \vec B = \frac{1}{\omega} \vec K \wedge \vec E\)
- A.1.3 -
\(- \vec K_1 . \vec r = - K_1 . (-\vec k) . \vec r = K_1 . z ~~~~ \Rightarrow ~~ \vec E_1 = E_{01} . \vec i . \exp \big[ \textrm{j} ( \omega . t + K_1. z ) \big]\)
\(\vec B_1 = \frac{1}{\omega} \vec K_1 \wedge \vec E_1 = \frac{K_1}{\omega} E_{01} . \exp \big[ \textrm{j} ( \omega . t + K_1 . z ) \big] . [- \vec k \wedge \vec i]\)
\(\Rightarrow ~~ \vec B_1 = - \frac{E_{01}}{\textrm{c}} . \vec j . \exp \big[ \textrm{j} ( \omega . t + K_1 . z ) \big]\)
- A.2 -
- A.2.1 -
L'onde réfléchie se propage dans le même milieu que l'incidente, donc à la même vitesse \(~~~~ \Rightarrow ~~\) même longueur d'onde : \(~~ \lambda_2 = \lambda_1 ~~~~ \Rightarrow ~~ K_2 = K_1\) .
Pour l'onde réfléchie : propagation suivant \((+ \vec k)\) \(~~~~ \Rightarrow ~~ \vec K_2 = - \vec K_1 = K_1 . \vec k ~~\) même direction de polarisation \(\vec i\) mais avec le déphasage \(\theta_2\) par rapport à \(\vec E_1\) .
\(\Rightarrow ~~ \vec E_2 = E_{02} . \exp \big[ \textrm{j} ( \omega . t + K_1 . z + \theta_2 ) \big] . \vec i\)
\(\vec B_2 = \frac{1}{\omega} \vec K_2 \wedge \vec E_2 ~~\) et \(~~ \vec K_2 \wedge \vec i = K_2 . \vec k \wedge \vec i = K_2 . \vec j\)
\(\Rightarrow ~~ \vec B_2 = \frac{E_{02}}{\textrm{c}} . \exp \big[ \textrm{j} ( \omega . t + K_1 . z + \theta_2 ) \big] . \vec j\)
Remarquer que \(\vec B_2\) se déduit directement de \(\vec E_2\) par la relation \(\vec B = \frac{1}{\omega} \vec K \wedge \vec E\) (valable pour les ondes planes monochromatiques) de sorte que le déphasage \(\theta_2\) est le même pour \(\vec E_2\) et pour \(\vec B_2\).
- A.2.2 -
Onde transmise : propagation suivant \((- \vec k)\) à la vitesse : \(v = \frac{\textrm{c}}{n}\) \(~~~~ \Rightarrow ~~ \vec K_3 = n \frac{\omega}{\textrm{c}} (- \vec k)\)
\(\vec E_3\) a même direction de polarisation que \(\vec E_1\) avec un déphasage \(\theta_3\)
\(\Rightarrow ~~ \vec E_3 = E_{03} . \exp \big[ \textrm{j} ( \omega . t + K_3 . z + \theta_3 ) \big] . \vec i\)
Comme précédemment : \(\vec B_3 = \frac{1}{\omega} \vec K_3 \wedge \vec E_3\)
\(\Rightarrow ~~ \vec B_3 = - n \frac{E_{03}}{\textrm{c}} . \vec j . \exp \big[ \textrm{j} ( \omega . t + K_3 . z + \theta_3 ) \big]\)
- A.3 -
- A.3.1 -
Les composantes normales de \(\vec E\) et de \(\vec B\) sont nulles \(~~~~ \Rightarrow ~~\) \(\vec E\) et \(\vec B\) sont tangentiels \(( \vec i , \vec j )\) .
\(\rightarrow ~~\) Pour \(\vec E\), on appelle \((1)\) :
\(\left \{ \begin{array}{ll} \textrm{Dans l'air :} \\ \vec E_{Ta} = \vec E_1 + \vec E_2 = E_{01} . \vec i . \exp \big[ \textrm{j} ( \omega . t + K_1. z ) \big] + E_{02} . \vec i . \exp \big[ \textrm{j} ( \omega . t - K_1. z + \theta_2) \big] \textrm{ } \\ \\ \textrm{Dans le verre :} \\ \vec E_{Tv} = \vec E_3 = E_{03} . \vec i . \exp \big[ \textrm{j} ( \omega . t + K_3 . z + \theta_3 ) \big] \end{array} \right.\)
\(\rightarrow ~~\) Pour \(\vec B\), on appelle \((2)\) :
\(\left\{ \begin{array}{lr} \textrm{Dans l'air :} \\ \vec B_{Ta} = \vec B_1 + \vec B_2 = \frac{E_{01}}{\textrm{c}} . (-\vec j) . \exp \big[ \textrm{j} ( \omega . t + K_1 . z ) \big] + \frac{E_{02}}{\textrm{c}} . \vec j . \exp \big[ \textrm{j} ( \omega . t - K_1 . z + \theta_2 ) \big] \textrm{ } \\ \\ \textrm{Dans le verre :} \\ \vec B_{Tv} = \vec B_3 = n \frac{E_{03}}{\textrm{c}} . ( - \vec j ) . \exp \big[ \textrm{j} ( \omega . t + K_3 . z + \theta_3 ) \big] \end{array} \right.\)
- A.3.2 -
Continuité en \(z = 0\)
\(\vec E_{Ta} = \vec E_{Tv}\)
\(\vec H_{Ta} = \vec H_{Tv}\) et \(\textrm{perm\'eabilit\'e magn\'etique pour l'air} = \textrm{pour le verre} = \mu_0\)
\(~~~~ \Rightarrow ~~ \vec B_{Ta} = \vec B_{Tv}\)
\((1) ~~~~ \Rightarrow ~~ [ E_{01} . \vec i . \exp (\textrm{j} . \omega . t) ] . \left[ 1 + \frac{E_{02}}{E_{01}} \exp (\textrm{j} . \theta_2) - \frac{E_{03}}{E_{01}} \exp (\textrm{j} . \theta_3) \right] = 0 ~~ \forall t ~~~~ \Rightarrow ~~ [...]_{(1)} = 0\)
\((2) ~~~~ \Rightarrow ~~ \left[ \frac{E_{01}}{\textrm{c}} . \vec j . \exp (\textrm{j} . \omega . t) \right] . \left[ -1 + \frac{E_{02}}{E_{01}} \exp (\textrm{j} . \theta_2) + n\frac{E_{03}}{E_{01}} \exp (\textrm{j} . \theta_3) \right] = 0 ~~ \forall t ~~~~ \Rightarrow ~~ [...]_{(2)} = 0\)
- A.3.3 -
En retranchant :
\([...]_{(1)} - [...]_{(2)} ~~~~ \Rightarrow ~~ 2 - (1+n) \frac{E_{03}}{E_{01}} \exp (\textrm{j} . \theta_3) = 0 ~~~~ \Rightarrow ~~ \frac{E_{03}}{E_{01}} \exp (\textrm{j} . \theta_3) =\frac{2}{1+n}\)
\(\Rightarrow ~~ T = \left( \frac{E_{03}}{E_{01}} \right)^2 = \frac{4}{(1+n)^2}\)
Remarquer que si les 2 milieux sont identiques (\(n= 1\)), on trouve bien : \(T = 1\) (toute l'énergie est transmise).
En ajoutant :
\([...]_{(2)} + n [...]_{(1)} ~~~~ \Rightarrow ~~ - (1-n) + (1+n) \frac{E_{02}}{E_{01}} \exp (\textrm{j} . \theta_2) = 0\)
\(\Rightarrow ~~ P = \left( \frac{n-1}{n+1} \right)^2\)
Remarquer que si \(n = 1\) (mêmes milieux), \(~~~~ \Rightarrow ~~ R = 0\) .
Remarque : En notant \(\vec S\) le vecteur de Poynting (avec les indices : \(i\) pour l'onde incidente, \(r\) pour l'onde réfléchie et \(t\) pour l'onde transmise), sachant que \(\mu_1 = \mu_2 = \mu_0\) (l'air et le verre sont non-magnétiques) et en remarquant que :
\(E_{01} . B_{01} = \frac{E_{01}^2}{\textrm{c}} ~\) , \(~~ E_{02} . B_{02} = \frac{E_{02}^2}{\textrm{c}} ~\) , \(~~ E_{03} . B_{03} = \frac{E_{03}^2}{v} = n \frac{E_{03}^2}{\textrm{c}} ~\)
On obtient :
\(\vec S_i + \vec S_r = \frac{E_1 . B_1}{\mu_1} - \frac{E_2 . B_2}{\mu_1} = \frac{E_1 . B_1}{\mu_0} \left[ 1 - \left(\frac{E_{02}}{E_{01}} \right)^2 \right]\)
d'où \(\vec S_i + \vec S_r = \frac{E_1 . B_1}{\mu_0} \left[ 1 - \left(\frac{n-1}{n+1}\right)^2\right] = \frac{E_1 . B_1}{\mu_0} \left[ \frac{4n}{(1+n)^2} \right]\)
De plus,
\(\vec S_t = \frac{E_3 . B_3}{\mu_2} = \frac{E_1 . B_1}{\mu_0} \frac{E_3 . B_3}{E_1 . B_1} = \frac{E_1 . B_1}{\mu_0} n \left[ \frac{4}{(1+n)^2} \right]\)
On a donc : \(\vec S_i + \vec S_r =\vec S_t\) : l'énergie de l'onde est conservée .
La réflexion (sur le dioptre plan) de l'onde électromagnétique incidente n'est pas totale : les champs électrique et magnétique réfléchis ont des amplitudes inférieures à celles des champs électrique et magnétique incidents.
La superposition des deux champs électriques et la superposition des deux champs magnétiques ne sont pas stationnaires.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
- B - Couche anti reflet.
- B.1 -
- B.1.1 -
\(\vec E_1 = E_{01} . \exp \big[ \textrm{j} ( \omega . t + K_1 . z ) \big] . \vec i\)
\(\vec B_1 = \frac{E_{01}}{\textrm{c}} . \exp \big[ \textrm{j} ( \omega . t + K_1 . z ) \big] . (-\vec j)\)
On a
\(\vec K_1 = K_1 . \vec k\) , avec \(~ K_1 = \frac{\omega}{\textrm{c}}\)
- B.1.2 -
\(\vec E_2 = E_{02} . \exp \big[ \textrm{j} ( \omega . t + K_2 . z + \theta_2) \big] . \vec i\)
\(\vec B_2 = n_1 \frac{E_{02}}{\textrm{c}} . \exp \big[ \textrm{j} ( \omega . t + K_2 . z + \theta_2) \big] . (-\vec j)\)
On a
\(\vec K_2 = - K_2 . \vec k\) , avec \(~ K_2 = n_1 \frac{\omega}{\textrm{c}}\)
- B.1.3 -
\(\vec E_3 = E_{03} . \exp \big[ \textrm{j} ( \omega . t + K_3 . z + \theta_3) \big] . \vec i\)
\(\vec B_3 = n \frac{E_{03}}{\textrm{c}} . \exp \big[ \textrm{j} ( \omega . t + K_3 . z + \theta_3) \big] . (-\vec j)\)
On a
\(\vec K_3 = - K_3 . \vec k\) , avec \(~ K_3 = n \frac{\omega}{\textrm{c}}\)
- B.1.4 -
\(\vec E_4 = E_{04} . \exp \big[ \textrm{j} ( \omega . t + K_2 . z + \theta_4) \big] . \vec i\)
\(\vec B_4 = n \frac{E_{04}}{\textrm{c}} . \exp \big[ \textrm{j} ( \omega . t + K_2 . z + \theta_4) \big] . (-\vec j)\)
On a
\(\vec K_4 = - \vec K_2 = K_2 . \vec k\)
- B.1.5 -
\(\vec E_5 = E_{05} . \exp \big[ \textrm{j} ( \omega . t + K_1 . z + \theta_5) \big] . \vec i\)
\(\vec B_5 = n \frac{E_{05}}{\textrm{c}} . \exp \big[ \textrm{j} ( \omega . t + K_1 . z + \theta_5) \big] . (-\vec j)\)
On a
\(\vec K_5 = - \vec K_1 = K_1 . \vec k\)
- B.2 -
- B.2.1 -
Continuité : tous les champs \(\vec E\) et \(\vec B\) sont tangentiels et, pour les trois milieux, \(\mu = \mu_0\) .
En \(z= 0 ~~ ( \forall t )\) :
\(\vec E_1 + \vec E_5 = \vec E_2 + \vec E_4\)
\(\vec B_1 + \vec B_5 = \vec B_2 + \vec B_4\)
\(E_{01} + E_{05} . \textrm{e}^{\textrm{j} . \theta_5} = E_{02} . \textrm{e}^{\textrm{j} . \theta_2} + E_{04} . \textrm{e}^{\textrm{j} . \theta_4} ~~~~ (1)\)
\(E_{01} - E_{05} . \textrm{e}^{\textrm{j} . \theta_5} = n_1 . E_{02} . \textrm{e}^{\textrm{j} . \theta_2} - n_1 . E_{04} . \textrm{e}^{\textrm{j} . \theta_4} ~~~~ (2)\)
En \(z= - e ~~ ( \forall t )\) :
\(\vec E_2 + \vec E_4 = \vec E_3\)
\(\vec B_2 + \vec B_4 = \vec B_3\)
\(E_{02} . \textrm{e}^{- \textrm{j} . K_2 . e} . \textrm{e}^{\textrm{j} . \theta_2} + E_{04} . \textrm{e}^{+ \textrm{j} . K_2 . e} . \textrm{e}^{\textrm{j} . \theta_4} = E_{03} . \textrm{e}^{- \textrm{j} . K_3 . e} . \textrm{e}^{\textrm{j} . \theta_3} ~~~~ (3)\)
\(n_1 . E_{02} . \textrm{e}^{- \textrm{j} . K_2 . e} . \textrm{e}^{\textrm{j} . \theta_2} - n_1 . E_{04} . \textrm{e}^{+ \textrm{j} . K_2 . e} . \textrm{e}^{\textrm{j} . \theta_4} = n . E_{03} . \textrm{e}^{- \textrm{j} . K_3 . e} . \textrm{e}^{\textrm{j} . \theta_3} ~~~~ (4)\)
- B.3 -
\(\frac{\omega . n_1 . e}{\textrm{c}} = \frac{\omega}{v} e = K_2 . e = K_4 . e\)
\(\Rightarrow ~~\) On pose : \(E_2 = E_{02} . \textrm{e}^{- \textrm{j} . K_2 . e}~~\) et \(~~ E_4 = E_{04} . \textrm{e}^{+ \textrm{j} . K_2 . e}\)
- B.3.1 -
En multipliant \((3)\) par \((-n)\) :
\(-n . ( E_2 .\textrm{e}^{\textrm{j} . \theta_2} + E_4 .\textrm{e}^{\textrm{j} . \theta_4} ) = - n .E_{03} . \textrm{e}^{+ \textrm{j} . K_3 . e} . \textrm{e}^{\textrm{j} . \theta_3}\)
On peut réécrire (4) :
\(n_1 . (E_2 . \textrm{e}^{\textrm{j} . \theta_2} - E_4 . \textrm{e}^{\textrm{j} . \theta_4}) = n . E_{03} . \textrm{e}^{- \textrm{j} . K_3 . e} . \textrm{e}^{\textrm{j} . \theta_3}\)
En ajoutant ces deux expressions, on obtient :
\((n_1 - n) . E_2 . \textrm{e}^{\textrm{j} . \theta_2} - (n_1 + n) . E_4 . \textrm{e}^{\textrm{j} . \theta_4} = 0\)
\(\Rightarrow ~~ E_4 = \frac{n_1 - 1}{n_1 + 1} E_2 . \textrm{e}^{\textrm{j} . (\theta_2 - \theta_4)} ~~~~(5)\)
- B.3.2 -
On suppose que l'épaisseur de la couche mince est : \(e = \frac{\lambda}{4}\) avec \(\lambda = \frac{2\pi}{K}\)
La couche mince est d'indice \(n_1\), d'où
\(K_2 = n_1 \frac{\omega}{\textrm{c}} ~~~~ \Rightarrow ~~ e = \frac{1}{4} \frac{2\pi}{K_2} ~~~~ \Rightarrow ~~ K_2 . e = n_1 \frac{\omega}{\textrm{c}} e = \frac{\pi}{2}\)
On a donc :
\(\textrm{e}^{+ \textrm{j} . K_2 . e} = \exp \left( \textrm{j} \frac{\pi}{2} \right) = \textrm{j} ~~~~ \Rightarrow ~~ E_4 = \textrm{j} . E_{04}\)
\(\textrm{e}^{- \textrm{j} . K_2 . e} = \exp \left( -\textrm{j} \frac{\pi}{2} \right) = -\textrm{j} ~~~~ \Rightarrow ~~ E_2 = - \textrm{j} . E_{02}\)
En portant ces valeurs dans la relation \((5)\) :
\(E_{04} = \frac{n - n_1}{n + n_1} E_{02} . \textrm{e}^{\textrm{j} . (\theta_2 - \theta_4)} ~~~~ (6)\)
- B.3.3 -
\((1) + (2)\) donne : \(~~ 2 E_{01} = (n_1 + 1) E_{02} . \textrm{e}^{\textrm{j} . \theta_2} + (1 - n_1) E_{04} . \textrm{e}^{\textrm{j} . \theta_4}\)
or, d'après \((6)\), on a : \((1 - n_1) E_{04} . \textrm{e}^{\textrm{j} . \theta_4} = (1 - n_1) \frac{n - n_1}{n + n_1} E_{02} . \textrm{e}^{\textrm{j} . \theta_2}\)
on a donc, en combinant ces deux résultats :
\(2 E_{01} = E_{02} . \textrm{e}^{\textrm{j} . \theta_2} \left[ (n_1 + 1) + (1 - n_1) \frac{n - n_1}{n + n_1} \right]\)
En développant :
\(E_{02} . \textrm{e}^{\textrm{j} . \theta_2} = E_{01} \frac{n + n_1}{n + n_1^2}\)
En reportant dans (6) :
\(E_{04} . \textrm{e}^{\textrm{j} . \theta_4} = \frac{n - n_1}{n + n_1^2} E_{01}\)
En portant ces valeurs dans (1) :
\(E_{01} + E_{05} . \textrm{e}^{\textrm{j} . \theta_5} = E_{01} \left[ \frac{n + n_1}{n + n_1^2} + \frac{n - n_1}{n + n_1^2} \right]\)
D'où :
\(E_{05} . \textrm{e}^{\textrm{j} . \theta_5} = E_{01} \left[ -1 + \frac{2n}{n + n_1^2} \right]\)
\(\Rightarrow ~~ \frac{E_{05}}{E_{01}} = \left[ -1 + \frac{2n}{n + n_1^2} \right] . \textrm{e}^{- \textrm{j} . \theta_5}\)
- B.3.4 -
\(R = \left| \frac{E_{05}}{E_{01}} \right|^2 = \left[ -1 + \frac{2n}{n + n_1^2} \right]^2\) , valable quelle que soit la longueur d'onde \(\lambda\) (pour les indices successifs \(1\), \(n_1\) et \(n\)).
La valeur minimale du coefficient de réflexion \(R\) est : \(R = 0\). Elle est obtenue pour : \(2 n = n + n_1^2\) , soit \(n_1 =\sqrt{n}\) .
Cette condition ne peut pas être satisfaite simultanément pour toutes les \(\lambda\) d'une lumière polychromatique, puisqu'elle est obtenue pour une couche dont l'épaisseur \(e\) est égale au \(\frac{1}{4}\) d'une longueur d'onde précisée : \(\lambda\) .
Complément de la question - B.3.2 -
En supposant que l'épaisseur est : \(e = \frac{\lambda}{4}\), on a montré la relation \((6)\) :
\(E_{04} = \frac{n - n_1}{n + n_1} E_{02} . \textrm{e}^{\textrm{j} . (\theta_2 - \theta_4)}\)
Supposons maintenant que l'épaisseur est : \(e = \frac{\lambda}{2}\)
\(\Rightarrow ~~ K_2 . e = \pi ~~~~ \Rightarrow \textrm{e}^{+ \textrm{j} . K_2 . e} = -1\)
\(\Rightarrow ~~\) Pour cette épaisseur : \(~ E_4 = - E_{04} ~\) et \(~ E_2 = - E_{02}\)
La relation \((5)\) précédente donne maintenant : \(E_{04} = \frac{n_1 - n}{n_1 + n} E_{02} . \textrm{e}^{\textrm{j} . (\theta_2 - \theta_4)}\)
\(\begin{array}{lllll} (1) + (2) & \Rightarrow & 2 E_{01} & = & (n_1 + 1) . \textrm{e}^{\textrm{j} . \theta_2} . E_{02} + (1 - n_1) . \textrm{e}^{\textrm{j} . \theta_4} . E_{04} \\ & \Rightarrow & 2E_{01} & =& (1 + n_1) . E_{02} . \textrm{e}^{\textrm{j} . \theta_2} + (1 - n_1) . \textrm{e}^{\textrm{j} . \theta_4} . \frac{n_1 - n}{n_1 + n} E_{02} . \textrm{e}^{\textrm{j} . (\theta_2 - \theta_4)} \\ & & & = & \bigg[ (1 + n_1) + \frac{(1 - n_1)(n_1 - n)}{(n_1 + n)} \bigg] E_{02} . \textrm{e}^{\textrm{j} . \theta_2} \\ & & & = & \frac{(1 + n_1)(n_1 + n) + (1 - n_1)(n_1 - n)}{(n_1 + n)} E_{02} . \textrm{e}^{\textrm{j} . \theta_2} \\ & & & = & \frac{n_1 + n_1^2 + n.n_1 + n_1 - n_1^2 - n + n.n_1}{n_1 + n} E_{02} . \textrm{e}^{\textrm{j} . \theta_2} \end{array}\)
Finalement, on a donc :
\(2 E_{01} = 2 n_1 \frac{1+n}{n_1 + n} E_{02} . \textrm{e}^{\textrm{j} . \theta_2}\)
\(\Rightarrow ~~ E_{01} = \frac{n_1(n+1)}{n_1 + n} E_{02} . \textrm{e}^{\textrm{j} . \theta_2}\)
On a donc avec \(E_{04}\) :
\(E_{04} . \textrm{e}^{\textrm{j} . \theta_4} = \frac{n-1}{n_1 + n} \frac{n + 1}{n_1 (n+1)} . E_{01}\)
\(\Rightarrow ~~ E_{04} . \textrm{e}^{\textrm{j} . \theta_4} = \frac{n-1}{n_1 (n + 1)} E_{01}\)
D'où :
\(E_1 + E_{05} . \textrm{e}^{\textrm{j} . \theta_5} = E_{01} \frac{n + 1}{n_1(n+1)} + \frac{n - 1}{n_1 (n + 1)} E_{01} = E_{01} \frac{n_1 + n + n_1 - n}{n_1 (n + 1)}\)
\(\Rightarrow ~~ E_{05} . \textrm{e}^{\textrm{j} . \theta_5} = \left( \frac{2}{n+1} - 1 \right) E_{01}\)
On en déduit :
\(E_{05} . \textrm{e}^{\textrm{j} . \theta_5} = \frac{1 - n}{1 + n} E_{01}\)
\(\Rightarrow ~~\) Pour cette épaisseur, le coefficient de réflexion est :
\(R = \left| \frac{E_{05}}{E_{01}} \right|^2 = \left[ \frac{1 - n}{1 + n} \right]^2\)