Flux d'énergie - onde progressive
Partie
Question
Question préliminaire : \(\vec e\) et \(\vec b\) étant des champs de vecteurs quelconques, démontrer la relation : \(div(\vec e\wedge\vec b)=\vec b.\vec{rot}(\vec e)-\vec e.\vec{rot}(\vec b)\)
On considère maintenant une onde électromagnétique : \((\vec E,\vec B)\) se propageant selon le vecteur unitaire \(\vec u\) dans un diélectrique homogène et isotrope de permittivité \(\varepsilon\) et de perméabilité \(\mu\). On se place en un point où la densité des charges et des courants est nulle \((r = 0, \vec j= \vec0)\). L'onde é.m. considérée est quelconque (non-nécessairement plane). En utilisant les équations de Maxwell, déduire de la relation précédente l'expression : \(div(\vec E\wedge\vec B)=-\frac{\partial}{\partial t}(\frac{B^2}{2}+\varepsilon.\mu\frac{E^2}{2})\) que l'on mettra sous la forme : \(div \vec S=\frac{\partial}{\partial t}(\frac{B^2}{2\mu}+\varepsilon\frac{E^2}{2})\) (\(\vec S\)=vecteur de Poynting)
Retrouver la relation (Cours : Flux d'énergie et impulsion d'une Onde Plane/Vecteur de Poynting) entre la variation de la quantité totale d'énergie localisée dans un volume \(t\) et le flux du vecteur de Poynting à travers la surface \(S\) qui délimite \(t\).
Montrer que dans le cas particulier de la propagation d'une onde é.m. plane, la densité d'énergie électrique est en tout point égale à la densité d'énergie magnétique.
Préciser en ce cas la direction et le sens du vecteur de Poynting.
Dans le cas particulier de la propagation d'une onde é.m. plane et harmonique, déterminer :
le vecteur de Poynting (en fonction de \(t\) et de la variable \(z\) dans le sens de la propagation),
la valeur moyenne au cours du temps et en tout point \(z\) de la densité d'énergie électrique et de la densité d'énergie magnétique,
la valeur moyenne dans tout l'espace et à tout instant \(t\) de la densité d'énergie électrique et de la densité d'énergie magnétique.
Commenter ces résultats.
L'ordre de grandeur de l'énergie solaire qui arrive sur terre par unité de temps et de surface est de \(\textrm{1000 W/m}^2\)
Calculer qu'elle est la valeur de \(E_o\) et \(B_o\) d'une onde plane harmonique qui délivrerait la même énergie. Comparer celles-ci aux valeurs des champs délivrés par une station de télévision à \(\textrm{1 km}\) de celle-ci, sachant que la station a une puissance \(P\) de \(\textrm{50 kW}\) et que l'émission est isotrope.
NB : Pour l'exercice -6- (ci-dessus), on utilisera la définition de l'intensité qui est l'énergie reçue par seconde et par unité de surface. La première question est relative à l'onde plane.
La seconde question est un problème de symétrie sphérique.
Justifier dans ce dernier cas que l'intensité sur une sphère de rayon \(R\) est reliée à la puissance de la source située au centre de cette sphère par la relation : \(I=\frac{P}{4\pi R^2}\)
Aide simple
Revoir la structure d'onde électromagnétique plane (qui permet d'exprimer le champ magnétique en fonction du champ électrique) et la définition du vecteur de Poynting.
Solution détaillée
1. Démonstration de la relation.
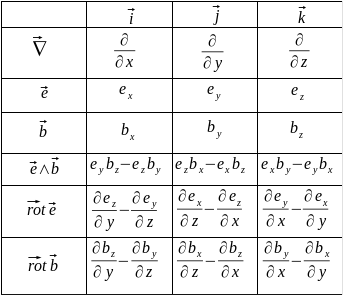
\(div~\vec e\land\vec b=\frac{\partial}{\partial x}[e_yb_z-e_zb_y]+\frac{\partial}{\partial y}[e_zb_x-e_xb_z]+\frac{\partial}{\partial z}[ e_xb_y-e_yb_x]\)
\(\vec b.\vec{rot}~\vec e=b_x[\frac{\partial e_z}{\partial y}-\frac{\partial e_y}{\partial z}]+b_y[\frac{\partial e_x}{\partial z}- \frac{\partial e_z}{\partial x}]+b_z[\frac{\partial e_y}{\partial x}-\frac{\partial e_x}{\partial y}]\)
\(\vec e.\vec{rot}~\vec b=e_x[\frac{\partial b_z}{\partial y}-\frac{\partial b_y}{\partial z}]+e_y[\frac{\partial b_x}{\partial z}- \frac{\partial b_z}{\partial x}]+e_z[\frac{\partial b_y}{\partial x}-\frac{\partial b_x}{\partial y}]\)
\(\vec b.\vec{rot}~\vec e-\vec e.\vec{rot}~\vec b=\begin{array} {l} -b_y\frac{\partial e_z}{\partial x}+b_z\frac{\partial e_y}{\partial x}+e_y\frac{\partial b_z}{\partial x}-e_z\frac{\partial b_y} {\partial z} \equiv \frac{\partial}{\partial x}[e_yb_z-e_zb_y] \\ -b_z\frac{\partial e_x}{\partial y}+b_x\frac{\partial e_z}{\partial y}+e_z\frac{\partial b_z}{\partial y}-e_x\frac{\partial b_z} {\partial y} \equiv \frac{\partial}{\partial y}[e_zb_x-e_xb_z] \\ -b_x\frac{\partial e_y}{\partial z}+b_y\frac{\partial e_z}{\partial y}+e_x\frac{\partial b_y}{\partial z}-e_y\frac{\partial b_x} {\partial z} \equiv \frac{\partial}{\partial z}[e_xb_y-e_yb_x] \end{array}\)
\(\Rightarrow\vec b.\vec{rot}~\vec e-\vec e.\vec{rot}~\vec b=div(\vec E\land\vec B)\)
Remarque : ces calculs sont longs et fastidieux et il est indispensable d'avoir un moyen de contrôle : vérifiez que les expressions ci-dessus peuvent se contrôler par permutation des indices, dans l'ordre \(x, y, z\) (cette permutation porte simultanément sur les indices et sur les variables de dérivation).
2. Pour démontrer la relation : \(div(\vec E\land\vec B)=-\frac{\partial}{\partial t}(\frac{B^2}{2}+\varepsilon\mu\frac{E^2}{2})\)
on applique la relation précédente aux champs électrique et magnétique :
\(\Rightarrow div(\vec E\land\vec B)=\vec B.\vec{rot}~\vec E-\vec E.\vec{rot}~\vec B\)
Maxwell (en dehors des courants) \(\Rightarrow \left|\begin{array}{l} \vec{rot}~\vec E=-\frac{\partial\vec B}{\partial t} \\ \vec{rot}~\vec B=\mu_0\vec j+\varepsilon\mu\frac{\partial\vec E}{\partial t}=\varepsilon\mu\frac{\partial\vec E} {\partial t} \end{array} \right.\)
\(\Downarrow\)
\(div(\vec E\land\vec B)=-\vec B.\frac{\partial\vec B}{\partial t}-\varepsilon\mu\vec E.\frac{\partial\vec E}{\partial t}=- \frac{1}{2}\frac{\partial}{\partial t}(B^2+\varepsilon\mu E^2)\)
Le vecteur de Poynting est : \(\vec S=\frac{1}{\mu}\vec E\land\vec B \Rightarrow div~\vec S=-\frac{\partial}{\partial t}(\frac{B^2}{2\mu}+\frac{\varepsilon E^2}{2})\)
3. La densité d'énergie dans un volume t est : \(w=\frac{B^2}{2\mu}+\frac{\varepsilon E^2}{2}\Rightarrow div~\vec S=-\frac{\partial}{\partial t}w\)
\(\Rightarrow \iiint_{(\tau)}div~\vec S.d\tau=-\frac{\partial}{\partial t}\iiint_{(\tau)}w.d\tau=-\frac{\partial W}{\partial t}\) où \(W\) est l'énergie contenue dans le volume (\(t\)).
4. L'onde qui se propage est plane \(\begin{array}{ll} \Rightarrow &\textrm{prenons }\quad \vec E\textrm{ selon }\vec i, ~ \vec B\textrm{ selon }\vec j \\ &\textrm{ et la propagation selon }\vec k \\\\ \Rightarrow & \vec B=\frac{1}{c}\vec u\land\vec E \quad \vec B=\frac{E}{c}\vec k\land\vec i=\frac{E}{c}\vec j \\ &\textrm{avec }\vec u=\vec k \quad \textrm{ et }\quad B=\frac{E}{c} \end{array}\)
\(W_{\textrm{\'elec}}=\frac{\varepsilon}{2}E_2\)
\(W_{magn}=\frac{B^2}{2\mu}=\frac{E^2}{c^22\mu}=\frac{\varepsilon E^2}{2c^2\varepsilon\mu}\) avec \(c=\frac{1}{\sqrt{\varepsilon\mu}}\Rightarrow c^2\varepsilon\mu=1\Rightarrow W_{magn}=\frac{\varepsilon}{2}E^2\)
\(\vec S=\frac{1}{\mu}\vec E\land\vec B\), \(\qquad\) \(\vec E\land\vec B\) est dans le sens du vecteur unitaire \(\vec u\) de la propagation.
5. On choisit la même orientation que dans la question précédente. La propagation de l'onde plane harmonique dans le sens de \(z\) croissant se représente par une fonction du type \(\cos(\omega t - Kz)\) [à un déphasage près que l'on peut choisir nul si les conditions initiales ne s'y opposent pas]
\(\left. \begin{array}{lll} E_x=E_0\cos(\omega t-Kz)\\\\ B_y=\frac{E_0}{c}\cos(\omega t-Kz)\end{array}\right| \begin{array}{lll} && \\\Rightarrow \vec S \textrm{ est sur } \vec k=\vec u :~ S_z &=& \frac{1}{\mu}E_x.B_y \\ &=& \frac{E_0^2}{\mu c}\cos^2(\omega t-Kz) \end{array}\)
\(\begin{array}{lll} \textrm{ Sachant que }\varepsilon \mu c^2=1&\Rightarrow &\frac{1}{\mu c}=\varepsilon ~c \\ &\Rightarrow &S_z=\frac{E^2_0}{\mu c}\cos^2(\omega t-Kz)\equiv c.\varepsilon E_x^2\equiv c[\frac{\varepsilon}{2}E_x^2+ \frac{B_y^2}{2\mu}]\equiv c~w \end{array}\)
Remarque :
On peut exprimer le flux de ce vecteur de Poynting \(\vec S=S_z\vec k\) à travers une surface fermée \((\Sigma)\) constituée d'un cylindre dont la génératrice est parallèle à \(Oz\) et de surface de base \(A\).
Le flux à travers la surface latérale du cylindre est donc nul et il ne reste que le flux à travers la surface \(A\) située en \(z\) et à travers la même surface \(A\) située en \(z+dz = z+ cdt\).(c= vitesse de l'onde).
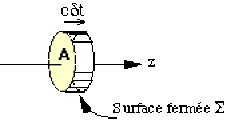
On peut considérer une surface \(A\) assez petite pour que \(S_z\) soit constant sur \(A\). Comme \(S_z = c w\), celà revient à supposer que \(w\) ne varie qu'avec \(t\) (ou qu'avec \(z\)).
\(\begin{array}{lll} \Rightarrow \iint_{(\Sigma)}\vec S\vec{d\Sigma}&=&\iint_{\Sigma}S_z\vec k.\vec{d\Sigma}=A.cw_{\textrm {en z}}-A.cw_{\textrm{en z}+\delta z} \\& =&-A.c\frac{\delta w}{\delta z}\delta z\equiv-A.c\frac{\delta w}{\delta t}\delta t \end{array}\)
\(w\) étant la densité d'énergie dans le volume (\(A. c.dt\)) délimité par la surface fermée (\(S\)), la quantité \((A. c.dt ).w\) est l'énergie \(W\) contenue dans (\(S\)).
\(\Rightarrow\iint_{(\Sigma)}\vec S.\vec{d\Sigma}=-(A.c.\delta t)\frac{\delta w}{\delta t}=-\frac{\delta W}{\delta t}\)
En faisant tendre \(\delta t\rightarrow0\), on retrouve ici le résultat général donné : \(\iint_{(\Sigma)}\vec S.\vec{d\Sigma}=-\frac{\partial W}{\partial t}\)
Valeurs moyennes. (notées : <...>)
\(<W_{\textrm{\'elec}}>=<W_{magn}>=\frac{\varepsilon}{2}<E^2>=\frac{\varepsilon}{2}E_0^2<\cos^2(\omega t-Kz)>\)
\(\cos^2\alpha=\frac{1}{2}[\cos^2\alpha+1]\Rightarrow<W_{\textrm{\'elec}}>=<W_{magn}> =\frac{\varepsilon E_0^2}{4}<(\cos^2(\omega t-Kz)+1)>\)
Moyenne dans le temps (sur \(\frac{T}{2}\))
\(=\int_{t_0}^{t_0+\frac{T}{2}}\cos^2(\omega t-Kz)dt=[\frac{\sin2(\omega t-Kz)} {2\omega}]_{t_0}^{t_0+\frac{T}{2}}=0\)
\(\Rightarrow\) il reste donc : \(<W_{\textrm{\'elec}}>=<W_{magn}>=\frac{\varepsilon E_0^2}{4}\)
Moyenne dans l'espace (sur \(\frac{\lambda}{2}\)) : on trouve de la même façon :
\(<W_{\textrm{\'elec}}>=<W_{magn}>=\frac{\varepsilon E_0^2}{4}\)
Remarquer que l'énergie électromagnétique se propage, puisque \(\vec S\) est une fonction de (\(\omega t-Kz\)), mais que ces valeurs moyennes restent constantes (ne dépendent ni de \(z\) ni de \(t\)).