Relation d'incertitude (2)
Partie
Question
Soit \(f(K)\) le spectre (sur la base des exponentielles imaginaires) d'une fonction \(\psi\) non périodique de variable \(z\), défini par :
\(f(K)=A\) pour \(K \in[\frac{K_0-\Delta K}{2},\frac{K_0+\Delta K}{2}]\), où \(\Delta K\) est quelconque
\(f(K)=0\) en dehors de cet intervalle.
Déterminer la fonction \(\psi(z)\) dont \(f(K)\) est le spectre.
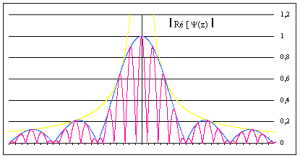
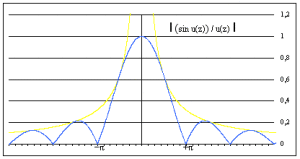
Représenter \(|\psi(z)|\)
En appelant \(\Delta z\) l'intervalle (entre \(2\) valeurs nulles de \(\psi\)) sur lequel la vibration \(\psi(z)\) présente une amplitude la plus importante, montrer la relation \(\Delta z.\Delta K=4\pi\).
Solution détaillée
Rappel :
\(\psi(z)=\int_{-\infty}^{+\infty}f(K)e^{iKz} . dK\) et \(f(K)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\psi(z) . e^{-iKz} . dz\)
1-
\(\psi(z)=\int_{K_0-\frac{\Delta K}{2}}^{K_0+\frac{\Delta K}{2}}e^{iKz}dK=\frac{A}{iz}e^{iK_0z}(e^{i\frac{\Delta K}{2}z}-e^{-i\frac{\Delta K}{2}z})=\frac{2A}{z}e^{iK_0z} . \frac{e^{i\frac{\Delta K}{2}z}-e^{-i\frac{\Delta K}{2}z}}{2i}\)
\(=\frac{2A}{z} . e^{ik_0z}\sin\frac{\Delta K}{2}z\)
\(\psi(z)=A . \Delta K . (e^{iK_0z}) . (\frac{\sin\frac{\Delta K}{2}z}{\frac{\Delta K}{2}z})\)
2-
\(\psi(z)=e^{iK_0z}\underbrace{(A . \Delta K(\frac{\sin\frac{\Delta K}{2}z}{\frac{\Delta K}{2} . z})}_{\textrm{partie réelle de }\psi(z)}\)
3-
Les valeurs \(+\pi\) et \(-\pi\) sont les premières qui annulent les sinus.
\(\frac{\Delta K}{2} . \Delta z=2\pi\Leftrightarrow \Delta K . \Delta z=4\pi\)
Remarque :
Passage à la limite :
spectre de raie \(\Rightarrow\) fonction périodique
spectre continu \(\Rightarrow\) fonction à support borné
Si \(\Delta K\rightarrow0 \Leftrightarrow \Delta z\rightarrow \infty\) fonction périodique de \(z\)
Si \(\Delta\omega\rightarrow0 \Leftrightarrow \Delta t\rightarrow \infty\) fonction périodique de \(t\)
Si \(\Delta K\rightarrow\infty \Leftrightarrow \Delta z\rightarrow 0\) fonction "impulsion" nulle partout sauf en un point \(z\)
Si \(\Delta\omega\rightarrow\infty \Leftrightarrow \Delta t\rightarrow 0\) fonction "impulsion" nulle partout sauf en un point \(t\)