Coefficient individuel de consanguinité f(X)
Dans une population supposée sans sélection, sans mutation, et d'effectif très grande on se propose de calculer f(x) : la probabilité que X ait reçu deux allèles identiques par ascendance provenant de l'ancêtre commun A.
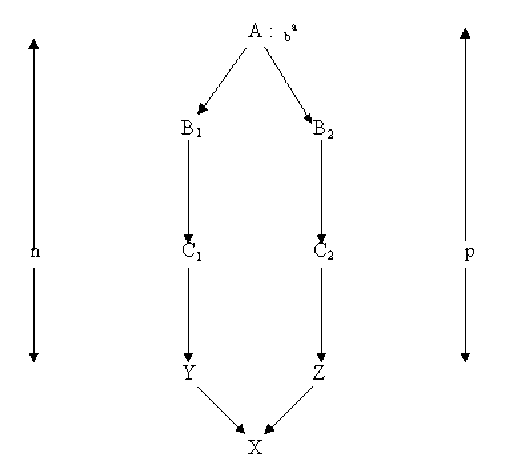
A : ancêtre commun à Y et Z
n : nombre de générations séparant A et Y (= chaînons de parenté)
p : nombre de générations séparant A et Z
ba : allèles d'un gène chez A
FA : coefficient de consanguinité de A
Il faut que :
L'allèle donné par Y à X vienne de A. Comme il y a deux allèles par locus, à chaque génération, la probabilité de transmission d'un allèle (a ou b) est \((1/2)^{n}\)
L'allèle donné par Z à X vienne de A : \((1/2)^{p}\)
"B1 et B2" reçoivent deux allèles identiques de A.
L'événement "B1 et B2" reçoivent deux allèles identiques de A peut se réaliser de deux manières différentes :
B1 et B2 reçoivent le même allèle de A (Prob : 1/2) et alors les deux allèles présents, l'un chez B1 et l'autre chez B2, sont nécessairement identiques,
ou
B1 et B2 reçoivent deux allèles différents de A (Pro : 1/2) ; ces deux allèles ne peuvent alors être identiques que si A est consanguin (\(f_{A}\)).
La probabilité que l'événement "B1 et B2" reçoivent deux allèles identiques de A est donc :
\(1/2 + 1/2 f(_{A}) = 1/2~( 1 + f(_{A}))\)
\(f(_{X}) = (1/2)^{n} . (1/2)^{p} . (1/2).(1 + f(_{A}))\)
Donc, \(\rightarrow f(_{X}) = (1/2)^{n+p+1} .~(1 + f(_{A}))\)
Cette formule s'appliquera autant de fois qu'il y aura d'ancêtres communs à X et autant de fois qu'il y aura de chaînes de parenté par ancêtre commun.
\(f(_{X}) = \sum{ (1/2 )^{n+p+1} .~(1 + f(A))}\)