Réactions opposées d'ordre 1 [Réactions composées]

Réactions opposées d'ordre 1

On appellera réaction directe la réaction $\mathbf{\textrm A\to\textrm B}$ et réaction inverse la réaction $\mathbf{\textrm B\to\textrm A}$ tout en remarquant que ce choix est arbitraire et que les termes de réactifs et de produits sont conventionnels et sont fixés par le choix des concentrations initiales en $\textrm A$ et $\textrm B$ .

Approche qualitative

Avant d'aborder l'étude analytique de la loi de vitesse, il est utile de se familiariser avec le comportement qualitatif du système cinétique.

Considérons pour commencer seulement la réaction directe $\mathbf{\textrm A\to\textrm B}$ d'ordre 1.

Soit $k_1$ son coefficient de vitesse et $C_{\textrm A0}$ la concentration initiale en $\textrm A$ .

La réaction est complète, au bout d'un certain temps, il ne reste pratiquement plus de réactif $\textrm A$ qui s'est entièrement transformé en $\textrm B$ .

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/anim52a.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

La réaction n'est donc pas complète, on atteint un état d'équilibre lorsque les vitesses des réactions directes et inverses sont égales, $\textrm v_1 = \textrm v_2$ .

D'où : $k_1.C_{\textrm A\infty} = k_{-1}.C_{\textrm B\infty}$ . Avec $C_{\textrm A\infty}$ et $C_{\textrm B\infty}$ respectivement les concentrations de $\textrm A$ et de $\textrm B$ à l'équilibre.

Qui s'écrit aussi : $\mathbf{\frac{k_1}{k_{-1}}=\frac{C_{\textrm B\infty}}{C_{\textrm A\infty}}}$

Dans le cas particulier considéré ci dessus où $k_1 = k_{-1}$ , on a évidemment $\mathbf{C_{\textrm A\infty} = C_{\textrm B\infty}}$ .

Exemple : Considérons maintenant le cas ou k1 > k-1.

$k_1 = \textrm{0,6 s}^{-1}$ (inchangé par rapport à ce qui précède) et $k_{-1} = \textrm{0,2 s}^{-1}$ .

En appliquant la relation précédente, il vient : $\mathbf{\frac{C_{\textrm B\infty}}{C_{\textrm A\infty}}=\frac{\textrm{0,6}}{\textrm{0,2}}}$

D'où $C_{\textrm B\infty} = 3.C_{\textrm A\infty}$

Comme $C_{\textrm A0} + C_{\textrm B0} = C_\textrm A + C_\textrm B = C_{\textrm A\infty} + C_{\textrm B\infty} = \textrm{1,0 mol.L}^{-1}$ .

Il vient aisément : $\mathbf{C_{\textrm A\infty} = \textrm{0,25 mol.L}^{-1}}$ et $\mathbf{C_{\textrm B\infty}= \textrm{0,75 mol.L}^{-1}}$ .

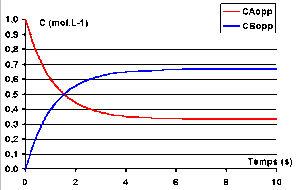
On obtient les courbes de variation des concentrations suivantes

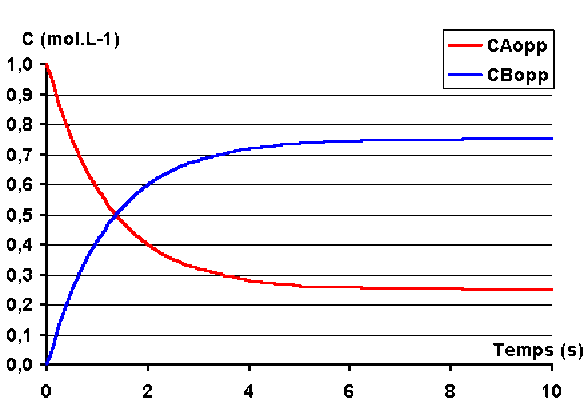
Notez que les courbes se coupent lorsque $C_\textrm A = C_\textrm B$ c'est-à-dire à $\mathbf{C_\textrm A=C_\textrm B = \textrm{0,5 mol.L}^{-1}}$ .

L'équilibre est quasiment atteint au bout de 7 ou 8 secondes.

Exemple : Considérons maintenant le cas ou k1 < k-1.

$k_1 = \textrm{0,6 s}^{-1}$ (inchangé par rapport à ce qui précède) et $k_{-1} = \textrm{1,8 s}^{-1}$ .

En appliquant la relation $\mathbf{\frac{k_1}{k_{-1}}=\frac{C_{\textrm B\infty}}{C_{\textrm A\infty}}}$

avec les données choisies, il vient $\frac{C_{\textrm B\infty}}{C_{\textrm A\infty}}=\frac{\textrm{0,6}}{\textrm{1,8}}$

d'où $C_{\textrm A\infty} = 3.C_{\textrm B\infty}$

Comme $C_{\textrm A0} + C_{\textrm B0} = C_\textrm A + C_\textrm B = C_{\textrm A\infty} + C_{\textrm B\infty} = \textrm{1,0 mol.L}^{-1}$ .

On trouve $\mathbf{C_{\textrm A\infty} = \textrm{0,75 mol.L}^{-1}}$ et $\mathbf{C_{\textrm B\infty} = \textrm{0,25 mol.L}^{-1}}$ .

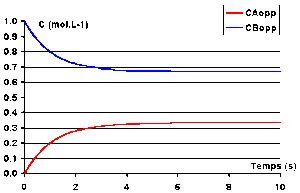
On obtient les courbes de variation des concentrations suivantes :

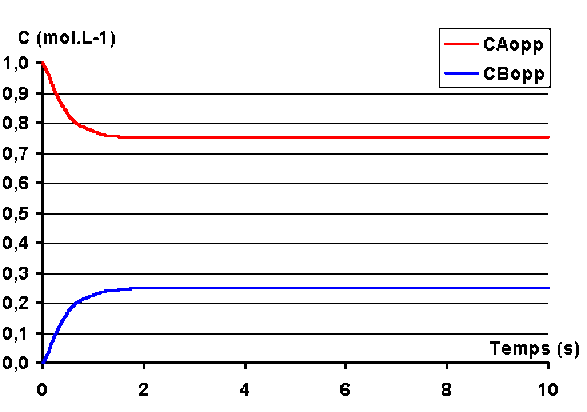
On note, que dans ce cas les courbes $C_\textrm A$ et $C_\textrm B$ ne se coupent pas.

En effet, la concentration à l'équilibre de $\textrm A$ , $C_\textrm{A,eq}$ est inférieure à 0,5 mol.L^-1 à aucun moment $C_\textrm A = C_\textrm B$ .

Notez également que l'équilibre est atteint plus rapidement que dans le cas précédent (au bout de 2 secondes environ). Cela vient du fait que la somme $k_1 + k_{-1}$ est supérieure à la valeur qu'elle avait dans le cas précédent. Ce point sera explicité lors de l'étude analytique de la loi de vitesse.

Etude analytique de la loi de vitesse

Soient $\textrm v_1$ et $\textrm v_{-1}$ les vitesses et $k_1$ et $k_{-1}$ les coefficients de vitesses des réaction directe et inverse.

Au temps $t = 0$ les concentrations initiales de $\textrm A$ et $\textrm B$ sont $C_{\textrm A0}$ et $C_{\textrm B0}$ .

Posons $x$ la concentration de $\textrm A$ transformée à l'instant $t$ .

Les concentrations courantes à cet instant $t$ sont : $C_\textrm A = C_{\textrm A0} - x$ et $C_\textrm B = C_{\textrm B0} + x$

La vitesse des réactions directe et inverse considérées isolément s'écrivent :

$\mathbf{\textrm v_1=k_1.C_\textrm A \textrm v_{-1}=k_{-1}.C_\textrm B}$

La vitesse globale de la réaction (définie comme étant la vitesse de disparition de $\textrm A$ ) est égale à :

$\mathbf{\textrm v=\frac{-\textrm dC_\textrm A}{\textrm dt}=\textrm v_1-\textrm v_{-1}}$

en effet $\textrm A$ disparaît par la réaction directe, mais se reforme par la réaction inverse.

Puisque la vitesse globale est définie comme étant la vitesse de disparition de $\textrm A$ , il faut compter positivement $\textrm v_1$ et négativement $\textrm v_{-1}$ .

D'où

$\mathbf{\textrm v=\frac{-\textrm dC_\textrm A}{\textrm dt}=\textrm v_1-\textrm v_{-1}=k_1.C_\textrm A-k_{-1}.C_\textrm B}$

et $\mathbf{\textrm v=\frac{-\textrm dC_\textrm A}{\textrm dt}=k_1.(C_{\textrm A0}-x)-k_{-1}.(C_{\textrm B0}+x)=\frac{\textrm dx}{\textrm dt}}$

Notez qu'on aboutit à la même expression si on définit la vitesse de la réaction comme étant égale à la vitesse de formation de $\textrm B$ .

En effet,

$\mathbf{\textrm v=\frac{-\textrm dC_\textrm A}{\textrm dt}=\frac{\textrm dx}{\textrm dt} \textrm{car} C_\textrm A=C_{\textrm A0}-x}$

$\mathbf{\textrm v=\frac{-\textrm dC_\textrm B}{\textrm dt}=\frac{\textrm dx}{\textrm dt} \textrm{car} C_\textrm B=C_{\textrm B0}+x}$

La loi de vitesse sous sa forme différentielle est donc

$\mathbf{\frac{\textrm dx}{\textrm dt}=k_1.(C_{\textrm A0}-x)-k_{-1}.(C_{\textrm B0}+x)}$

L'intégration de cette équation conduit à la loi de vitesse sous sa forme intégrée :

$\mathbf{\ln\frac{x_\infty}{x_\infty-x}=(k_1+k_{-1}).t}$

Cliquez ici^[1] pour voir les détails sur l'intégration de la loi de vitesse.

Remarque :

Dans l'expression de la loi de vitesse sous sa forme intégrée $\mathbf{\ln \frac{x_\infty}{x_\infty - x} = ( k_1 + k_{-1} ).t}$ , $x_\infty$ représente la concentration de $\textrm A$ transformée entre l'état initial et l'équilibre. Puisque $C_\textrm A = C_{\textrm A0} - x_\infty$ , $x_\infty$ peut donc se déterminer facilement à partir de $C_{\textrm A0}$ et de $C_{\textrm A\infty}$ .
L'expression de la loi de vitesse sous sa forme intégrée $\mathbf{\ln \frac{x_\infty}{x_\infty - x} = ( k_1 + k_{-1} ).t}$ est identique à une loi de vitesse dont le coefficient de vitesse serait $k_\textrm{obs} = k_1 + k_{-1}$ et dont la concentration initiale en $\textrm A$ aurait été $x_\infty$ . C'est donc la somme $k_1 + k_{-1}$ qui a un effet direct sur la vitesse avec laquelle le système évolue vers l'équilibre ainsi que nous l'avons observé qualitativement.

Influence des valeurs des coefficients de vitesse sur le régime cinétique

Voyons de nouveau quelques situations typiques :

Influence de la somme $k_1 + k_{-1}$ , le rapport $\frac{k_1}{k_{-1}}$ étant maintenu constant.

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/k1surk2_cte.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

Influence du rapport $\frac{k_1}{k_{-1}}$ , la somme $k_1 + k_{-1}$ étant maintenue constante.

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/k1plusk2_cte.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

Influence des concentrations initiales sur le régime cinétique

Dans les exemples qui précèdent nous avons considéré que la concentration initiale en $\textrm B$ était nulle.

Il est évident que l'opérateur a le choix des concentrations initiales.

En particulier il est (du moins en principe) possible d'étudier la réaction en partant du produit $\textrm B$ et en prenant $C_{\textrm A0} = 0$ .

Les rôles de $\textrm A$ et de $\textrm B$ se trouvent alors inversés. $\textrm B$ peut alors être considéré comme le réactif et $\textrm A$ comme le produit. Les graphes suivants représentent les variations de concentrations obtenues pour des mêmes valeurs des coefficients de vitesse quand on intervertit les concentrations initiales de $\textrm A$ et $\textrm B$ .

$K_1 = \textrm{0,6 s}^{-1}$

$K_{-1} = \textrm{0,3 s}^{-1}$

$C_{\textrm A0} = \textrm{1,0 mol.L}^{-1}$

$C_{\textrm B0} = \textrm{0,0 mol.L}^{-1}$

$K_1 = \textrm{0,6 s}^{-1}$

$K_{-1} = \textrm{0,3 s}^{-1}$

$C_{\textrm A0} = \textrm{0,0 mol.L}^{-1}$

$C_{\textrm B0} = \textrm{1,0 mol.L}^{-1}$

Les coefficients de vitesse étant les mêmes, on obtient évidemment le même état d'équilibre. Mais les concentrations initiales étant permutées, dans un cas les courbes se coupent, dans l'autre non.

Il est également possible de démarrer la réaction avec un mélange de $\textrm A$ et de $\textrm B$ .

Pour illustrer les conséquences sur le régime cinétique, nous tracerons quelques graphes pour les mêmes valeurs de : $K_1$ et $K_{-1}$ en faisant varier le rapport $\frac{C_{\textrm A0}}{C_{\textrm B0}}$ tout en maintenant la somme $C_{\textrm A0} + C_{\textrm B0}$ constante et égale à 1 mol.L^-1.

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/ca_plus_cb_cte.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

On constate que lorsque les concentrations initiales se rapprochent des concentrations dans l'état d'équilibre, la réaction est de moins en moins importante.

Plus précisément $x_\infty = C_{\textrm A0} - C_{\textrm A\infty}$ tend vers 0.

$x_\infty$ représente en quelque sorte la concentration de $\textrm A$ "transformable", on l'appelle parfois la concentration "cinétiquement active".

Lorsque les concentrations initiales sont égales aux concentrations à l'équilibre, c'est-à-dire lorsque $x_\infty = 0$ , l'état d'équilibre est établit d'emblée et il n'y a pas de réaction décelable au niveau macroscopique.

$K_1 = \textrm{0,6 s}^{-1}$

$K_{-1} = \textrm{0,3 s}^{-1}$

$C_{\textrm A0} = \textrm{0,33 mol.L}^{-1}$

$C_{\textrm B0} = \textrm{0,66 mol.L}^{-1}$

Remarques sur l'état d'équilibre

Remarque : Nature de l'état d'équilibre

L'état d'équilibre atteint par le système au bout d'un certain temps est un équilibre dynamique.

Au niveau macroscopique, la composition du système ne varie plus.

Cependant au niveau microscopique, la réaction ne s'est pas arrêtée.

Pendant chaque intervalle de temps, un certain nombre de molécules de $\textrm A$ se transforment en molécules de $\textrm B$ . Dans le même temps, un nombre égal de molécules de $\textrm B$ se transforment en molécule de $\textrm A$ . Les vitesses des réactions directes et inverses sont égales.

cine2_ab_ba_orange.param [param]

Cet état d'équilibre dynamique ne doit pas être confondu avec un mélange inerte. Dans un mélange inerte, la composition du système ne varie évidemment pas, elle est fixée par les quantités de constituants introduits dans le mélange. Dans un équilibre dynamique, la composition n'évolue pas, précisément parce qu'on est dans l'état d'équilibre. La composition dépend de la valeur de la constante d'équilibre et des concentrations initiales des réactifs.

Remarque : Perturbation de l'état d'équilibre (approfondissement)...

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/anim52e.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

Remarque : Relation entre coefficients de vitesse et constante d'équilibre

Lorsque l'équilibre est atteint, les vitesses des réactions directes et inverses sont égales.

Ce qui s'exprime par : $\textrm v_1 = k_1.C_{\textrm A\infty} = \textrm v_{-1} = k_{-1}.C_{\textrm B\infty}$

d'où $\mathbf{\frac{k_1}{k_{-1}}=\frac{C_{\textrm B\infty}}{C_{\textrm A\infty}}}$ .

Or le rapport $\frac{C_{\textrm B\infty}}{C_{\textrm A\infty}}$ n'est autre que la constante d'équilibre exprimée en concentration $K_c$

$\mathbf{K_c=\frac{C_{\textrm B\infty}}{C_{\textrm A\infty}}}$ d'où $\mathbf{K_c=\frac{k_1}{k_{-1}}}$ .

Nota : s'agissant d'un rapport sans dimension, ce rapport est aussi égal à la constante thermodynamique d'équilibre $K$ et à la constante d'équilibre exprimée en pression, $K_p$ , puique dans ces conditions, les valeurs de ces trois constantes sont égales.

Rappel :

La valeur de la constante thermodynamique d'équilibre $K_T$ à une température donnée $T$ , se calcule à partir de la variation d'enthalpie libre de référence de la réaction à la même température $\Delta_\textrm RG^{\circ}_T$ par la relation: $\mathbf{R.T.\ln K_T = -\Delta_\textrm RG^{\circ}_T}$ .

Traitement des données expérimentales

L'objectif est double :

Vérifier que la réaction obéit bien aux lois de vitesses correspondant au schéma cinétique.
Déterminer les valeurs des coefficients de vitesse.

Selon les données dont on dispose, on utilise la loi de vitesse sous sa forme différentielle ou sous sa forme intégrée.

Utilisation de la loi de vitesse sous sa forme différentielle
$\mathbf{\textrm v = \frac{-\textrm dC_\textrm A}{\textrm dt} = \textrm v_1 - \textrm v_{-1} = K_1.C_\textrm A - K_{-1}. C_\textrm B}$
Pour utiliser la loi de vitesse sous cette forme, il faut disposer de plusieurs valeurs de la vitesse de réaction pour diverses valeurs des concentrations $C_\textrm A$ et $C_\textrm B$ .
Un cas particulièrement simple se présente si on a mesuré les vitesses initiales et que l'on a fait deux séries d'expériences, l'une avec $C_{\textrm A0}$ différent de 0 et $C_{\textrm B0} = 0$ , l'autre avec $C_{\textrm A0} = 0$ et $C_{\textrm B0}$ différent de 0. La première série permet de déterminer $k_1$ , la seconde $k_{-1}$ .
On peut aussi mesurer la vitesse et les concentrations $C_\textrm A$ et $C_\textrm B$ au cours du temps sur une seule expérience. Il en résulte une série de relations que l'on résout pour déterminer $k_1$ et $k_{-1}$ . L'utilisation des vitesses est simple, mais donne des résultats assez peu précis, car la détermination des vitesse (souvent effectuée par dérivation graphique des courbes concentration / temps) est délicate et imprécise.

Exemple : Utilisation des vitesses initiales

On étudie la réaction équilibrée $\mathbf{\textrm A \textrm{}^\to_\gets \textrm B}$ en faisant deux séries de trois expériences.

Première série d'expériences avec une concentration initiale en $\textrm B$ nulle $C_{\textrm B0} = 0$ .

La seconde avec une concentration initiale en $\textrm A$ nulle $C_{\textrm A0} = 0$ .

On ne mesure que la variation de concentration en $\textrm A$ .

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/exemple_5_2_f1.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

Deuxième série d'expériences.

Bien que la première série d'expérience ait permis de valider le modèle et de déterminer les coefficients de vitesse, nous traiteront de manière similaire la deuxième série d'expériences afin de voir s'ils confirment les résultats obtenus.

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/exemple_5_2_f1_2.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

Remarque :

Dans cet exemple, on a utilisé des données calculées avec au min trois chiffres significatifs, les résultats obtenus sont en parfait accord. En pratique, les mesures expérimentales sont difficile et il est exceptionnel que l'on puisse atteindre une telle précision. Une déviation de l'ordre de 5 à 10 % n'est pas rare, et il ne faudra pas conclure trop vite au rejet du modèle cinétique dans de telles situations.

Exemple : Utilisation des vitesses au cours du temps

On utilise ici les résultats d'une seule expérience au cours de laquelle on détermine, à différents instants, la valeur de la vitesse et de la concentration d'un ou des deux réactifs. Considérons par exemple une expérience réalisée avec $C_{\textrm A0} = \textrm{0,15 mol.L}^{-1}$ et $C_{\textrm B0} = 0 \textrm{mol.L}^{-1}$ .

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/exemple_5_2_f1_3.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

Utilisation de la loi de vitesse sous sa forme intégrée
La forme intégrée de la loi de vitesse s'écrit :
$\mathbf{\ln\frac{x_\infty}{x_\infty - x} = ( k_1 + k_{-1} ).t}$
avec $x_\infty= C_{\textrm A0} - C_{\textrm A\infty}$
et $\mathbf{\frac{k_1}{k_{-1}}=\frac{C_{\textrm B\infty}}{C_{\textrm A\infty}}}$
On détermine d'abord $x_\infty$ à partir de $C_{\textrm A0}$ et $C_{\textrm A\infty}$ .
Notez que, dans certain cas, la composition à l'équilibre, donc $C_{\textrm A\infty}$ peut être connue ou déterminée séparément.
Puis on vérifie la relation $\mathbf{\ln\frac{x_\infty}{x_\infty - x} = ( k_1 + k_{-1} ).t}$ soit par une méthode graphique, soit en vérifiant que la valeur de $k_1 + k_{-1}$ calculée pour une série de points est constante. Enfin, connaissant $k_1 + k_{-1}$ et le rapport $\frac{k_1}{k_{-1}}$ (par la composition à l'équilibre), on calcule séparément les valeurs de chaque coefficient de vitesse.

Exemple : Utilisation de la loi de vitesse sous sa forme intégrée

On étudie une réaction opposée avec $C_{\textrm A0} = \textrm{0,0056 mol.L}^{-1}$ et $C_{\textrm B0} = 0\textrm{ mol.L}^{-1}$ . On obtient les variations de concentrations de $\textrm A$ et de $\textrm B$ suivantes :

Impossible d'accéder à la ressource audio ou vidéo à l'adresse : https://uel.unisciel.fr/chimie/cinet/cinet_ch06/res/exemple_5_2_f2.mp4

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

Exemples de réactions.

Exemple : Enolisation d'une β-dicétone en système conjugué :

Exemple : Isomérisation E / Z du 1,2-biphényle éthylène :

Notes

Réactions opposées - Détail intégration
L'équation
$\mathbf{\frac{\textrm dx}{\textrm dt} = k_1.(C_{\textrm A0} - x) - k_{-1}.(C_{\textrm B0} + x)}$
se développe en
$\mathbf{\frac{\textrm dx}{\textrm dt} = k_1.C_{\textrm A0} - k_{-1}.C_{\textrm B0} - (k_1 + k_{-1}).x}$
on cherche ensuite a factoriser $(k_1 + k_{-1})$ . Il vient :
$\mathbf{\frac{\textrm dx}{\textrm dt} = (k_1 + k_{-1}).\Big[\frac{ k_1.C_{\textrm A0} - k_{-1}.C_{\textrm B0}}{k_1 + k_{-1}} - x\Big]}$
On remarque que cette équation a la même forme que la loi de vitesse d'une réaction du premier ordre en posant :
$\mathbf{k_\textrm{obs} = k_1 + k_{-1} \textrm{et} C_\infty = \frac{ k_1.C_{\textrm A0} - k_{-1}.C_{\textrm B0}}{k_1 + k_{-1}}}$
on obtient : $\frac{\textrm dx}{\textrm dt} = k_\textrm{obs}.(C_\infty - x)$ qui s'identifie bien à $\frac{\textrm dx}{\textrm dt} = k.( C_0 - x)$ de la loi du premier ordre dont l'intégration est facile et donne :
$\mathbf{\ln\frac{C_\infty}{C_\infty - x} = k_\textrm{obs}.t}$
Que représente le terme $C_\infty$ ?
On a posé :
$\mathbf{C_\infty = \frac{k_1.C_{\textrm A0} - k_{-1}.C_{\textrm B0}}{k_1 + k_{-1}}}$
qui se développe en :
$\mathbf{C_\infty . (k_1 + k_{-1}) = k_1.C_{\textrm A0} - k_{-1}.C_{\textrm B0}}$
puis
$\mathbf{k_1.(C_{\textrm A0} - C_\infty ) = k_{-1}.(C_{\textrm B0} + C_\infty )}$
On remarque que les deux membres de cette égalité sont égaux à l'expression des vitesses des réactions directe $\textrm v_1 = k_1.(C_{\textrm A0} - x)$ et inverse $\textrm v_{-1} = k_{-1}.(C_{\textrm B0} + x)$ dans lesquelles $C_\infty$ serait emplacé par $x$ .
Ces deux vitesses ne sont égales qu'à l'équilibre c'est-à-dire au temps $t = \infty$ .
$C_\infty$ est donc égal à $x_\infty$ c'est-à-dire à la concentration de $\textrm A$ disparue à l'équilibre.
L'expression intégrée peut donc s'écrire :
$\mathbf{\ln \frac{x_\infty}{x_\infty - x}= ( k_1 + k_{-1} ).t}$