Infra Rouge

Le spectre Infra Rouge d'une molécule résulte de transitions entre ses différents états vibrationnels. Parmi ces vibrations, les oscillations ou élongations, associant les mouvements relatifs de deux atomes séparés par une liaison, sont parmi les plus significatives. Pour faciliter l'étude de ce type de vibrations, on a généralement recours au modèle physique de l'oscillateur harmonique.

Le recours au modèle de l'oscillateur harmonique consiste à assimiler les deux atomes à un système constitué de deux corps \(\textrm C_1\) et \(\textrm C_2\) de masses ponctuelles respectives \(\textrm m_1\) et \(\textrm m_2\) (\(\textrm m_1 = \textrm m_2 = \textrm m\) , si les deux atomes sont identiques) reliées par un ressort de raideur \(\textrm k\). A partir de ce modèle, il est facile d'établir les relations associant la fréquence des vibrations du système aux deux grandeurs le caractérisant c'est-à-dire les masses et la raideur du ressort.

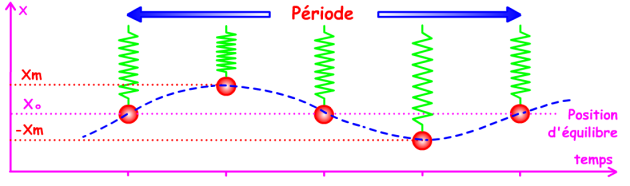
La théorie de l'oscillateur harmonique s'appuie, dans une approche simple, sur le mouvement d'une seule masse fixée à un ressort. A la suite d'une compression ou d'un étirement du ressort, cette masse va entamer un mouvement périodique, oscillant autour de la longueur standard du ressort (.....de la longueur de liaison en IR).

Le nombre d'oscillations par unité de temps, c'est-à-dire la fréquence, est donné par la relation :

\(\mathrm{N=\frac{1}{2.\pi}\sqrt{\frac{k}{m}}}\)

N s'exprime en Hertz (Hz)

Retenez cette formule, elle « explique » beaucoup de comportements en IR !

Cette fréquence, caractéristique de chaque oscillateur, est à la base de l'interprétation des bandes d'élongation en spectroscopie Infra Rouge !

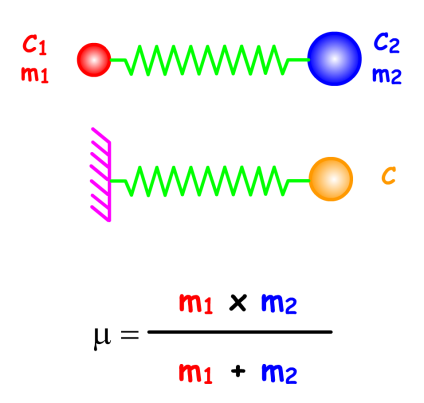
En fait, ces modèles simples ne sont pas directement utilisables pour formaliser le comportement des molécules car celles-ci ne sont pas attachées à un point fixe. On est donc amené à envisager un modèle un peu plus complexe.

Soient \(\textrm C_1\) et \(\textrm C_2\) deux corps de masses respectives \(\textrm m_1\) et \(\textrm m_2\), reliés l'un à l'autre par un ressort de raideur \(\textrm k\). Il est facile de montrer qu'un tel système possède la même fréquence et la même énergie potentielle que le système précédent dans lequel la masse du corps \(\textrm C\) est égale à la masse réduite \(\textrm m\) des deux corps.