Effet d'écran dans le modèle de champ moyen
Partie
Question
On considère l'atome d'hélium dans le modèle de champ moyen. Sa configuration électronique dans l'état fondamental est \(1\mathrm{s}^2\).
On cherche l'orbitale 1s sous la forme suivante :
\(\psi_{1s}\left(\mathrm{r},\theta,\phi\right)=\frac{1}{\sqrt\pi}\left(\frac{\alpha}{\mathrm{a_0}}\right)^{\frac{3}{2}}\exp\left(-\frac{\alpha\mathrm{r}}{\mathrm{a}_0}\right)\)
L'énergie E associée à l'état fondamental n'est pas une somme d'énergie d'orbitales. On peut montrer qu'elle s'exprime en unité atomique comme :
\(\mathrm{E}=2\mathrm{I+J}\)
avec
\(\mathrm{I}=\frac{1}{2}\left(\alpha^2-2\mathrm{Z\alpha}\right)\)
\(\mathrm{J}=\frac{5}{8}~\alpha\)
\(\mathrm{I}\) est l'énergie associée à un électron sur l'orbitale 1s ; \(\mathrm{J}\) est l'énergie de répulsion entre les deux électrons.
1. Déterminer la valeur de \(\alpha\). Quelle est sa signification physique ?
2. Représenter la densité radiale associée à l'orbitale 1s de \(\mathrm{He}\) et la comparer à celle du cation hydrogénoïde \(\mathrm{He}^+\). On calculera le rayon le plus probable dans les deux cas.
On donne :\( \mathrm{a}_0=0,529~\AA\)
Aide simple
Le sens physique du paramètre \(\alpha\) a trait aux forces qui s'exercent sur l'électron décrit par l'orbitale 1s.
La densité radiale est la densité de probabilité sur une sphère de rayon \(\mathrm{r}\). Pour une orbitale de symétrie sphérique, elle s'exprime comme :
\(\mathrm{D}\left(\mathrm{r}\right)=4\pi~\mathrm{r^2}\vert\psi\vert^2\)
Aide méthodologique
1. Il s'agit de déterminer pour quelle valeur de \(\alpha\) l'énergie de l'atome est minimale.
2. Il faut savoir exprimer la densité radiale d'une orbitale 1s de symétrie sphérique.
Le rayon le plus probable correspond au maximum de la densité radiale
Aide à la lecture
Le paramètre \(\alpha\) est le paramètre variationnel dans ce problème.
Solution détaillée
1. On applique le principe des variations.
On cherche le minimum de l'énergie E de l'atome par rapport à \(\alpha\). Il suffit d'annuler la dérivée première :
\(\frac{\mathrm{dE}}{\mathrm{d}\alpha}=2\alpha-2\mathrm{Z}+\frac{5}{8}=0\)
soit : \(\alpha=\mathrm{Z}-\frac{5}{16}=2-\frac{5}{16}=\frac{27}{16}=1,6875\)
\(\alpha\) est la charge effective qui attire l'électron, compte tenu de la répulsion de l'autre électron qui fait écran à l'attraction du noyau.
On peut ainsi estimer la constante d'écran \(\sigma_{1s/1s}=\mathrm{Z}-\alpha=0,3125\), qui est très proche de celle proposée par Slater dans le modèle plus simple qui porte son nom.
2. La densité radiale pour une orbitale 1s de symétrie sphérique est égale au produit de la densité en un point de la sphère par la surface de la sphère :
\(\mathrm{D}_{1s}\left(\mathrm{r}\right)=4\pi\mathrm{r}^2\vert\psi_{1s}\vert^2=4\mathrm{r}^2\left(\frac{\alpha}{\mathrm{a}_0}\right)^3\exp\left(-2\frac{\alpha\mathrm{r}}{\mathrm{a_0}}\right)\)
Pour le cation hydrogénoïde \(\mathrm{He}^+\), \(\alpha=\mathrm{Z}=2\). Les courbes sont représentées ci-dessous. La densité pour l'orbitale 1s de \(\mathrm{He}\) possède une extension plus importante et son maximum est déporté vers les grandes valeurs de \(\mathrm{r}\).
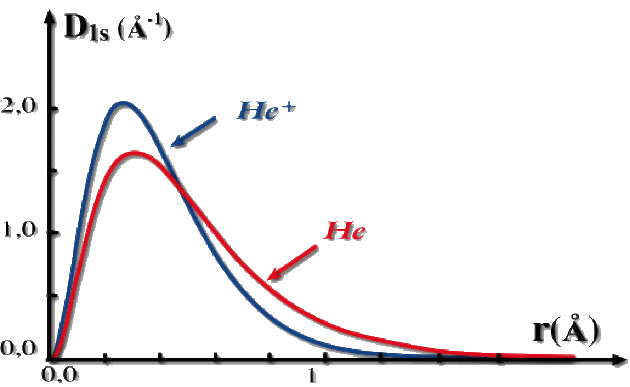
Le rayon le plus probable correspond au maximum de la densité radiale. On cherche les extrémas :
\(\frac{\mathrm{d}}{\mathrm{dr}}\left(\mathrm{D_{1s}}\right)=4\left(\frac{\alpha}{\mathrm{a_0}}\right)^3\exp\left(-2\frac{\alpha\mathrm{r}}{\mathrm{a_0}}\right)\left[\mathrm{r}-\frac{\alpha}{\mathrm{a_0}}\right]=0\)
Le maximum est en \(\mathrm{r}=\frac{\mathrm{a_0}}{\alpha}\). Le rayon le plus probable est donc situé en :
\(\mathrm{r}=\frac{\mathrm{a_0}}{\alpha}=\frac{0,529}{1,6875}=0,313\AA\) pour \(\mathrm{He}\)
\(\mathrm{r}=\frac{\mathrm{a_0}}{\mathrm{Z}}=\frac{0,529}{2}=0,2645\AA\) pour \(\mathrm{He^+}\)
La présence de deux électrons sur l'orbitale 1s la rend donc plus diffuse que l'orbitale hydrogénoïde. Cette respiration de l'orbitale traduit la répulsion entre les deux électrons.